Video: Wie findet man die zweite Ableitung einer trigonometrischen Funktion?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
VIDEO
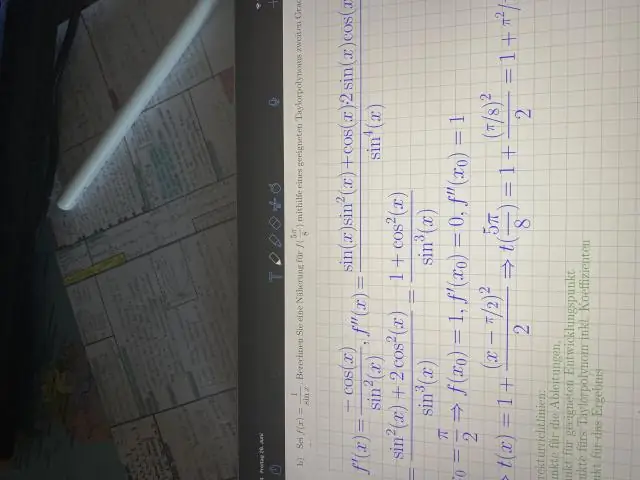
Also, was sind die Ableitungen der 6 trigonometrischen Funktionen?
Ableitungen trigonometrischer Funktionen. Die grundlegenden trigonometrischen Funktionen umfassen die folgenden 6 Funktionen: Sinus ( Sünde x), Kosinus ( cos x), Tangente (tanx), Kotangens (cotx), Sekante (secx) und Kosekans (cscx). Alle diese Funktionen sind stetig und in ihren Domänen differenzierbar.
Anschließend stellt sich die Frage, was ist die Ableitung von 1? Die Derivat sagt uns die Steigung einer Funktion an einem beliebigen Punkt. Es gibt Regeln, denen wir folgen können, um viele zu finden Derivate . Beispiel: Die Steigung eines konstanten Wertes (wie 3) ist immer 0.
Derivat Regeln.
| Gemeinsame Funktionen | Funktion | Derivat |
|---|---|---|
| Konstante | C | 0 |
| Leitung | x | 1 |
| Axt | ein | |
| Quadrat | x2 | 2x |
Die Leute fragen auch, was ist die 27. Ableitung von COSX?
Sünde
Was ist cos 2x?
cos ( 2x ) = cos (x + x) = cos (x) cos (x) - sin(x)sin(x) = cos ^ 2(x ) - Sünde^ 2(x ) Angesichts der pythagoräischen Identitäten: (sünde^ 2(x ) + cos ^ 2(x ) = 1), cos ^ 2(x ) = 1 - Sünde^ 2(x ) so cos ( 2x ) ist auch gleich (1 - Sünde^ 2(x )) - Sünde^ 2(x ) oder 1 - 2sin^ 2(x )
Empfohlen:
Wie findet man die Tangentengleichung einer Ableitung?
1) Finden Sie die erste Ableitung von f(x). 2) Setzen Sie den xvalue des angegebenen Punktes in f '(x) ein, um die Steigung bei x zu finden. 3) Setzen Sie den x-Wert in f(x) ein, um die y-Koordinate des Tangentenpunkts zu finden. 4) Kombinieren Sie die Steigung aus Schritt 2 und den Punkt aus Schritt 3 mit der Punkt-Neigungs-Formel, um die Gleichung für die Tangente zu finden
Wie findet man die symbolische Darstellung einer quadratischen Funktion?
Quadratische Funktionen können symbolisch durch die Gleichung y(x) = ax2 + bx + c dargestellt werden, wobei a, b und c Konstanten sind und a ≠ 0. Dieses Formular wird als Standardformular bezeichnet
Wie findet man die Gleichung einer Geraden aus einem Punkt und einer Parallelen?
Die Geradengleichung in der Steigungs-Schnittpunkt-Form ist y=2x+5. Die Steigung der Parallellinie ist gleich: m=2. Die Gleichung der Parallellinie lautet also y=2x+a. Um a zu finden, benutzen wir die Tatsache, dass die Linie durch den gegebenen Punkt gehen soll:5=(2)⋅(−3)+a
Wie findet man a in einer quadratischen Funktion?
Die quadratische Funktion f(x) = a(x - h)2 + k, a ungleich Null, heißt in Standardform. Wenn a positiv ist, öffnet sich der Graph nach oben, und wenn a negativ ist, öffnet er sich nach unten. Die Symmetrielinie ist die vertikale Linie x = h und der Scheitelpunkt ist der Punkt (h,k)
Wie findet man den Maximalwert einer quadratischen Funktion?
Wenn Sie die Formel y = ax2 + bx + c erhalten, können Sie den Maximalwert mit der Formel max = c- (b2 / 4a) ermitteln. Wenn Sie die Gleichung y = a(x-h)2 + k haben und Theaterm negativ ist, dann ist der Maximalwert k