Video: Wie findet man den Maximalwert einer quadratischen Funktion?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
Wenn Sie die Formel y = ax2 + bx + c erhalten, können Sie die höchster Wert mit der Formel max =c- (b2 / 4a). Wenn Sie die Gleichung y = a(x-h)2 + k haben und das Theaterm negativ ist, dann ist die höchster Wert ist k.
Wenn man dies berücksichtigt, wie findet man den Minimalwert einer quadratischen Gleichung?
Wenn dein quadratische Gleichung hat ein positives aterm, es wird auch a. haben Mindestwert . Du kannst finden Dies Mindestwert indem Sie die Funktion grafisch darstellen oder eine der beiden verwenden Gleichungen . Wenn du das hast Gleichung in der Form von y = ax^2 + bx + c, dann kannst du Finde den Mindestwert Verwendung der Gleichung min = c-b^2/4a.
Und was ist das Maximum in Mathematik? Maximum, In Mathematik , ein Punkt, an dem der Wert einer Funktion am größten ist. Wenn der Wert größer oder gleich allen anderen Funktionswerten ist, handelt es sich um einen absoluten maximal . Wenn es nur größer als ein nahegelegener Punkt ist, ist es ein relativer oder lokaler, maximal.
Man kann sich auch fragen, was ist der Maximalwert einer Funktion?
Die Maximalwert einer Funktion ist der Ort, an dem Funktion erreicht seinen höchsten Punkt oder Scheitelpunkt in einem Diagramm. In diesem Bild beispielsweise ist der höchster Wert des Funktion ist y gleich 5. In der Praxis findet das Maximalwert einer Funktion kann verwendet werden, um zu bestimmen maximal Gewinn oder maximal Bereich.
Was ist das Maximum einer Funktion?
Eine kontinuierliche Funktion kann annehmen a maximal an einem einzigen Punkt oder kann Maxima an mehreren Punkten aufweisen. Global maximal von a Funktion ist der größte Wert im gesamten Bereich der Funktion , und ein Einheimischer maximal ist der größte Wert in einer lokalen Nachbarschaft.
Empfohlen:
Wie findet man den Skalierungsfaktor einer Dilatation auf einer Koordinatenebene?
Zeichnen Sie das Dreieck ABC mit den Koordinaten A(2, 6), B(2, 2), C(6, 2). Dann dilatieren Sie das Bild um einen Skalierungsfaktor von 1/2 mit dem Ursprung als Zentrum der Dilatation. Zuerst zeichnen wir unser ursprüngliches Dreieck in der Koordinatenebene. Als nächstes multiplizieren wir jede Koordinate mit dem Skalierungsfaktor von 1/2
Wie findet man die symbolische Darstellung einer quadratischen Funktion?
Quadratische Funktionen können symbolisch durch die Gleichung y(x) = ax2 + bx + c dargestellt werden, wobei a, b und c Konstanten sind und a ≠ 0. Dieses Formular wird als Standardformular bezeichnet
Wie findet man a in einer quadratischen Funktion?
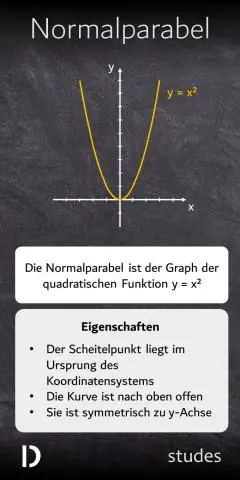
Die quadratische Funktion f(x) = a(x - h)2 + k, a ungleich Null, heißt in Standardform. Wenn a positiv ist, öffnet sich der Graph nach oben, und wenn a negativ ist, öffnet er sich nach unten. Die Symmetrielinie ist die vertikale Linie x = h und der Scheitelpunkt ist der Punkt (h,k)
Wie findet man den nächsten Term in einer quadratischen Folge?
Schreiben Sie den n-ten Term dieser quadratischen Zahlenfolge auf. Schritt 1: Bestätigen Sie, ob die Sequenz quadratisch ist. Dies geschieht durch das Finden des zweiten Unterschieds. Schritt 2: Wenn Sie die zweite Differenz durch 2 teilen, erhalten Sie den Wert von a
Wie findet man den Definitionsbereich einer algebraischen Funktion?
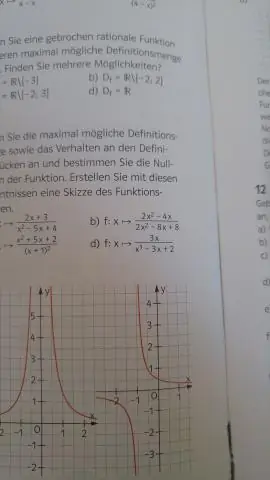
Der Definitionsbereich einer Funktion ist die Menge aller möglichen Eingaben für die Funktion. Zum Beispiel sind der Bereich von f(x)=x² alle reellen Zahlen und der Bereich von g(x)=1/x sind alle reellen Zahlen außer x=0