Video: Wie findet man die symbolische Darstellung einer quadratischen Funktion?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
Quadratische Funktionen kann symbolisch dargestellt werden durch die Gleichung , y(x) = ax2 + bx + c, wobei a, b und c Konstanten sind und a 0. Diese Form wird als Standardform bezeichnet.
Die Leute fragen auch, was ist die symbolische Darstellung einer Funktion?
Funktionen . Sie kennen wahrscheinlich am besten die symbolische Darstellung von Funktionen , wie die Gleichung y = f(x). Funktionen kann durch Tabellen dargestellt werden, Symbole , oder Grafiken.
Wie bestimmt man die Form eines quadratischen Graphen? Form der Parabel
- Wenn a>0, dann hat die Parabel einen minimalen Punkt und sie öffnet sich nach oben (U-förmig) z.
- Wenn a<0, dann hat die Parabel einen maximalen Punkt und sie öffnet sich nach unten (n-förmig) z.
- (a) Überprüfen Sie, ob a>0 oder a<0 ist, um zu entscheiden, ob es U-förmig oder n-förmig ist.
- (c) Die Koordinaten des y-Achsenabschnitts (Ersatz x=0).
Wie stellt man dementsprechend eine quadratische Funktion dar?
Grafiken. EIN quadratische Funktion ist eine der Form f(x) = ax2 + bx + c, wobei a, b und c Zahlen mit a ungleich Null sind. Der Graph von a quadratische Funktion ist eine Kurve, die als Parabel bezeichnet wird. Parabeln können sich nach oben oder unten öffnen und in "Breite" oder "Steilheit" variieren, aber sie haben alle die gleiche grundlegende "U"-Form.
Wie löst man eine Funktion?
Zum Funktionen , die beiden Notationen bedeuten genau dasselbe, aber "f (x)" gibt Ihnen mehr Flexibilität und mehr Informationen. Du sagtest immer "y = 2x + 3; lösen für y wenn x = –1". Jetzt sagen Sie "f (x) = 2x + 3; find f (-1)" (ausgesprochen als "f-of-x ist gleich 2x plus drei; find f-of-negative-one").
Empfohlen:
Wie findet man die zweite Ableitung einer trigonometrischen Funktion?
VIDEO Also, was sind die Ableitungen der 6 trigonometrischen Funktionen? Ableitungen trigonometrischer Funktionen. Die grundlegenden trigonometrischen Funktionen umfassen die folgenden 6 Funktionen: Sinus ( Sünde x), Kosinus ( cos x), Tangente (tanx), Kotangens (cotx), Sekante (secx) und Kosekans (cscx).
Wie findet man a in einer quadratischen Funktion?
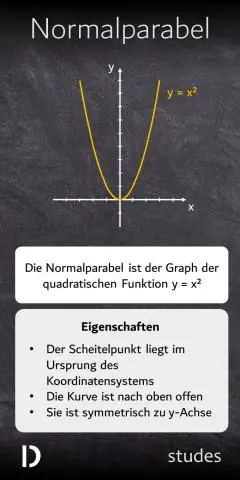
Die quadratische Funktion f(x) = a(x - h)2 + k, a ungleich Null, heißt in Standardform. Wenn a positiv ist, öffnet sich der Graph nach oben, und wenn a negativ ist, öffnet er sich nach unten. Die Symmetrielinie ist die vertikale Linie x = h und der Scheitelpunkt ist der Punkt (h,k)
Wie findet man den nächsten Term in einer quadratischen Folge?
Schreiben Sie den n-ten Term dieser quadratischen Zahlenfolge auf. Schritt 1: Bestätigen Sie, ob die Sequenz quadratisch ist. Dies geschieht durch das Finden des zweiten Unterschieds. Schritt 2: Wenn Sie die zweite Differenz durch 2 teilen, erhalten Sie den Wert von a
Wie findet man den Maximalwert einer quadratischen Funktion?
Wenn Sie die Formel y = ax2 + bx + c erhalten, können Sie den Maximalwert mit der Formel max = c- (b2 / 4a) ermitteln. Wenn Sie die Gleichung y = a(x-h)2 + k haben und Theaterm negativ ist, dann ist der Maximalwert k
Was ist die symbolische Darstellung einer Funktion?
Funktionen. Sie kennen wahrscheinlich die symbolische Darstellung von Funktionen wie die Gleichung y = f(x). Funktionen können durch Tabellen, Symbole oder Grafiken dargestellt werden