- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:33.
- Zuletzt bearbeitet 2025-01-22 16:55.
Es gibt drei grundlegende starre Transformationen : Reflexionen, Rotationen und Translationen. Reflexionen reflektieren die Form über eine gegebene Linie. Drehungen drehen eine Form um einen gegebenen Mittelpunkt. Übersetzungen verschieben oder verschieben eine Form von einem Ort zum anderen.
Was ist außerdem eine starre Transformation in der Mathematik?
Mathematik Definition von Starre Transformationen : Starre Transformationen - EIN Transformation das die Größe oder Form einer Figur nicht verändert; Rotationen, Reflexionen, Translationen sind alles starre Transformationen . Gegenstand: Mathematik . Thema: Geometrie.
Und was sind die 4 Arten von Transformationen? Es gibt vier Haupttypen von Transformationen: Übersetzung , Drehung , Betrachtung und Dilatation.
Was ist außerdem ein Beispiel für eine starre Transformation?
Reflexionen, Translationen, Rotationen und Kombinationen dieser drei Transformationen sind " starre Transformationen ". Eine Reflexion heißt a starre Transformation oder Isometrie, da das Bild die gleiche Größe und Form wie das Vorbild hat.
Welche drei Arten von starren Transformationen gibt es?
Eine grundlegende starre Transformation ist eine Bewegung der Form, die sich nicht auf die Größe der Form auswirkt. Die Form schrumpft nicht oder wird größer. Es gibt drei grundlegende starre Transformationen: Reflexionen , Drehungen , und Übersetzungen . Es gibt eine vierte allgemeine Transformation, die Dilatation genannt wird.
Empfohlen:
Warum verwenden wir Transformationen?

Transformationen sind nützlich, weil sie das Verständnis des Problems in einem Bereich einfacher machen als in einem anderen. Oder Sie transformieren es in den S-Bereich (Laplacetransform) und lösen die Schaltung mit einfacher Algebra und konvertieren dann Ihre Ergebnisse aus dem S-Bereich zurück in den Zeitbereich (inverse Laplace-Transformation)
In welcher Reihenfolge wenden Sie Transformationen an?
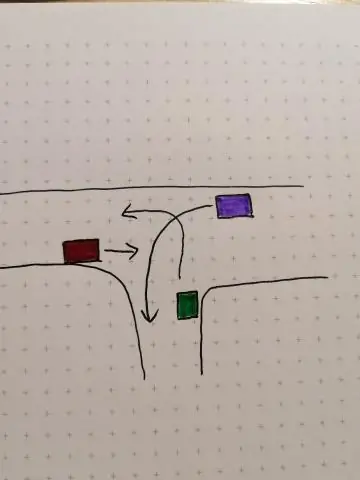
Wenden Sie die Transformationen in dieser Reihenfolge an: Beginnen Sie mit Klammern (achten Sie auf eine mögliche horizontale Verschiebung) (Dies könnte eine vertikale Verschiebung sein, wenn die Potenz von x nicht 1 ist) Umgang mit Multiplikation (Streckung oder Kompression) Umgang mit Negation (Reflexion) Umgang mit Addition/Subtraktion (vertikale Verschiebung)
Ist die Dilatation eine nicht starre Transformation?

Eine Dilatation ist eine Transformation, die ein Bild erzeugt, das dieselbe Form wie das Original hat, aber eine andere Größe hat. Hinweis: Eine Dilatation wird NICHT als starre Transformation (oder Isometrie) bezeichnet, da das Bild NICHT unbedingt die gleiche Größe wie das Vorbild hat (und starre Transformationen die Länge erhalten)
Ist die Transformation eine starre Bewegung?

Starre Bewegung wird auch als starre Transformation bezeichnet und tritt auf, wenn ein Punkt oder ein Objekt bewegt wird, Größe und Form jedoch gleich bleiben. Dies unterscheidet sich von einer nicht starren Bewegung, wie einer Dilatation, bei der die Größe des Objekts zunehmen oder abnehmen kann
Was bedeutet Macht zu einer Macht?

Definition. Ein anderes Wort, das verwendet wird, um einen Exponenten zu beschreiben, ist Macht. Wenn Sie also den Ausdruck potenzieren hören, bedeutet dies nur, einen Exponenten zu einem anderen zu erheben. Egal in welcher Form der Exponent auftritt, die gleiche Regel gilt für die Berechnung einer Potenz in eine Potenz. Die Regel ist, die Exponenten miteinander zu multiplizieren
