Video: Wie findet man den Scheitelpunkt einer horizontalen Parabel?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
Wenn eine Parabel hat ein horizontal Achse, die Standardform der Gleichung der Parabel ist das: (y-k)2 = 4p(x - h), wobei p≠ 0. Die Scheitel von diesem Parabel ist bei (h, k). Der Fokus liegt bei (h + p, k). Thedirectrix ist die Linie x = h - p.
Wie findet man den Scheitelpunkt und die Leitlinie einer Parabel?
Die Standardform ist (x - h)2 = 4p (y - k), wobei die Fokus ist (h, k + p) und die Direktion ist y = k - p. Wenn die Parabel wird so gedreht, dass es Scheitel ist (h, k) und seine Symmetrieachse ist parallel zur x-Achse, es hat an Gleichung von (y - k)2 = 4p (x -h), wobei die Fokus ist (h + p, k) und die Direktion ist x = h - p.
Wie lautet außerdem die Gleichung für eine Seitwärtsparabel? Die "allgemeine" Form von a Parabelgleichung ist die, an die Sie gewöhnt sind, y = ax2 + bx + c - es sei denn, das Quadrat ist " seitwärts ", in welchem Fall die Gleichung sieht ungefähr so aus wie x = ay2 + von +c.
Wie findet man den Scheitelpunkt einer Parabelgleichung?
Dieser Punkt, an dem die Parabel ändert die Richtung, wird als " Scheitel ". Wenn das Quadrat in der Form y = a(x – h) geschrieben wird2 + k, dann die Scheitel ist der Punkt (h, k). Das macht Sinn, wenn man darüber nachdenkt. Der quadratische Teil ist immer positiv (für eine rechte Seite nach oben) Parabel ), es sei denn, es ist null.
Für welchen Wert von p hat der Scheitelpunkt der Parabel?
Das Absolute Wert von p ist der Abstand zwischen Scheitel und der Fokus und der Abstand zwischen den Scheitel und die Leitlinie. (Die Anmeldung P sagt mir, auf welche Weise die Parabel Gesichter.) Da Fokus und Leitlinie zwei Einheiten voneinander entfernt sind, muss dieser Abstand eine Einheit betragen, also | P | = 1.
Empfohlen:
Wie findet man den Skalierungsfaktor einer Dilatation auf einer Koordinatenebene?
Zeichnen Sie das Dreieck ABC mit den Koordinaten A(2, 6), B(2, 2), C(6, 2). Dann dilatieren Sie das Bild um einen Skalierungsfaktor von 1/2 mit dem Ursprung als Zentrum der Dilatation. Zuerst zeichnen wir unser ursprüngliches Dreieck in der Koordinatenebene. Als nächstes multiplizieren wir jede Koordinate mit dem Skalierungsfaktor von 1/2
Wie findet man die Gleichung einer Geraden aus einem Punkt und einer Parallelen?
Die Geradengleichung in der Steigungs-Schnittpunkt-Form ist y=2x+5. Die Steigung der Parallellinie ist gleich: m=2. Die Gleichung der Parallellinie lautet also y=2x+a. Um a zu finden, benutzen wir die Tatsache, dass die Linie durch den gegebenen Punkt gehen soll:5=(2)⋅(−3)+a
Wie beschriftet man den Scheitelpunkt und die Symmetrieachse?
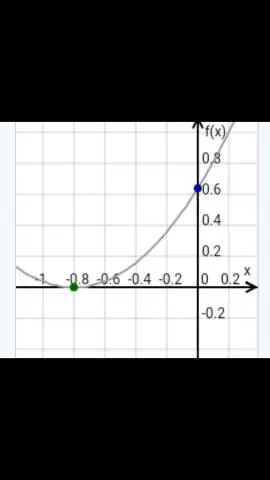
Die Symmetrieachse geht immer durch den Scheitel der Parabel. Die x-Koordinate des Scheitelpunkts ist die Gleichung der Symmetrieachse der Parabel. Für eine quadratische Funktion in Standardform, y=ax2+bx+c, ist die Symmetrieachse eine vertikale Linie x=−b2a
Wie findet man den pH-Wert am Äquivalenzpunkt einer starken Säure und einer starken Base?
Am Äquivalenzpunkt verbinden sich gleiche Mengen H+ und OH- zu H2O, was zu einem pH-Wert von 7,0 (neutral) führt. Der pH-Wert am Äquivalenzpunkt für diese Titration beträgt immer 7,0. Beachten Sie, dass dies nur für Titrationen von starken Säuren mit starken Basen gilt
Wie findet man den Definitionsbereich einer Restriktion in einer Gleichung?
Gewusst wie: Bei einer gegebenen Funktion, die in einer Gleichungsform geschrieben ist, die einen Bruch enthält, finden Sie die Domäne. Identifizieren Sie die Eingabewerte. Identifizieren Sie alle Einschränkungen für die Eingabe. Wenn die Formel der Funktion einen Nenner enthält, setze den Nenner gleich Null und löse nach x