Inhaltsverzeichnis:
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:32.
- Zuletzt bearbeitet 2025-06-01 05:03.
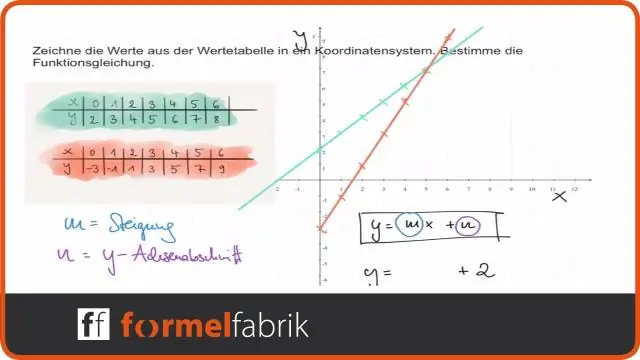
Gewusst wie: Gegeben die Gleichung von a lineare Funktion , verwenden Transformationen grafisch darstellen lineare Funktion in der Form f(x)=mx+b f(x) = mx+b. Graph f(x)=x f(x) = x. Dehnen oder komprimieren Sie den Graphen vertikal um den Faktor |m|. Verschieben Sie die Grafik um b Einheiten nach oben oder unten.
Also, wie beschreibt man die Transformation einer linearen Funktion?
Der Graph von a lineare Funktion (eine Linie) kann um das Koordinatengitter verschoben werden. Dies nennt man a Transformation . Es gibt drei grundlegende Transformationen : Translation (die Linie verschieben), Reflexion (die Linie umdrehen) und skalieren (die Linie strecken). Du kannst dich bewegen ( verwandeln ) die Linie vertikal oder horizontal.
Welche Transformationen beeinflussen außerdem die Steigung einer linearen Funktion? Transformieren Lineare Funktionen (Stretch and Compression) Dehnungen und Kompressionen verändern die Steigung einer linearen Funktion . Wenn die Linie steiler wird, wird die Funktion vertikal gestreckt oder horizontal gestaucht wurde.
Wie transformiert man dementsprechend eine Funktion?
Die Funktionsübersetzungs- / Transformationsregeln:
- f (x) + b verschiebt die Funktion um b Einheiten nach oben.
- f (x) - b verschiebt die Funktion um b Einheiten nach unten.
- f (x + b) verschiebt die Funktion b Einheiten nach links.
- f (x - b) verschiebt die Funktion b Einheiten nach rechts.
- -f (x) spiegelt die Funktion in der x-Achse wider (also auf dem Kopf stehend).
Wie spiegelt man eine Funktion wider?
EIN Funktion kann sein reflektiert um eine Achse durch Multiplizieren mit minus eins. Zu reflektieren um die y-Achse multiplizieren Sie jedes x mit -1, um -x zu erhalten. Zu reflektieren um die x-Achse multiplizieren Sie f(x) mit -1, um -f(x) zu erhalten.
Empfohlen:
Wie ähneln sich lineare Ungleichungen und lineare Gleichungen?

Das Lösen linearer Ungleichungen ist dem Lösen linearer Gleichungen sehr ähnlich. Der Hauptunterschied besteht darin, dass Sie das Ungleichheitszeichen umdrehen, wenn Sie mit einer negativen Zahl dividieren oder multiplizieren. Bei der grafischen Darstellung linearer Ungleichungen gibt es noch einige weitere Unterschiede. Der schattierte Teil enthält die Werte, bei denen die lineare Ungleichung wahr ist
Wie wertet man zusammengesetzte Funktionen aus?
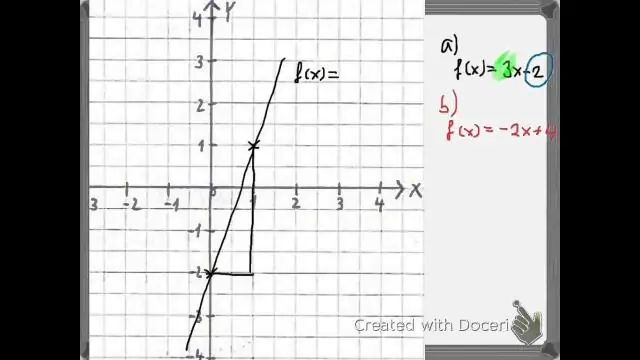
Auswerten zusammengesetzter Funktionen mithilfe von Graphen Lokalisieren Sie die gegebene Eingabe für die innere Funktion auf der x-Achse ihres Graphen. Lesen Sie die Ausgabe der inneren Funktion von der y-Achse ihres Graphen ab. Lokalisieren Sie die Ausgabe der inneren Funktion auf der x-Achse des Graphen der äußeren Funktion
Wie multipliziert man zusammengesetzte Funktionen?

Multiplikation und Zusammensetzung von Funktionen Um eine Funktion mit einem Skalar zu multiplizieren, multiplizieren Sie jede Ausgabe mit diesem Skalar. Wenn wir f (g(x)) nehmen, nehmen wir g(x) als Eingabe der Funktion f. Wenn zum Beispiel f (x) = 10x und g(x) = x + 1 sind, dann finden wir, um f (g(4)) zu finden, g(4) = 4 + 1 + 5 und berechnen dann f (5 ) = 10(5) = 50. Beispiel: f (x) = 2x - 2, g(x) = x2 - 8
Wie findet man Arc-Trigger-Funktionen?

Wir bezeichnen die Umkehrfunktion als y=sin&1(x). Es wird gelesen, dass y die Umkehrung von Sinus x ist und bedeutet, dass y der reelle Zahlenwinkel ist, dessen Sinuswert x ist. Achten Sie auf die verwendete Schreibweise. Graphen von inversen trigonometrischen Funktionen. Funktionsbereich csc−1(x) (−∞,−1]∪[1,∞) [−π2,0)∪(0,π2]
Was sind einige Beispiele aus der Praxis für lineare Funktionen?

Ursprünglich beantwortet: Könnte mir jemand ein Beispiel für eine reale Situation mit linearen Funktionen geben? Lineare Funktionen treten immer dann auf, wenn Sie eine konstante Änderungsrate haben. Beispiele aus dem wirklichen Leben sind: Ermittlung des Stromverbrauchs an Tag 1,2,3… Sie nehmen ein Auto zur Miete. Sie fahren ein Auto mit einer Geschwindigkeit von 60 km/h
