Inhaltsverzeichnis:
Video: Wie wertet man zusammengesetzte Funktionen aus?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
Auswerten zusammengesetzter Funktionen mit Graphen
- Suchen Sie die angegebene Eingabe in das innere Funktion auf der x-Achse seines Graphen.
- Lesen Sie die Ausgabe des inneren. ab Funktion von der y-Achse seines Graphen.
- Finde das Innere Funktion Ausgabe auf der x-Achse des Graphen der äußeren Funktion .
Wie schreibt und bewertet man hier zusammengesetzte Funktionen?
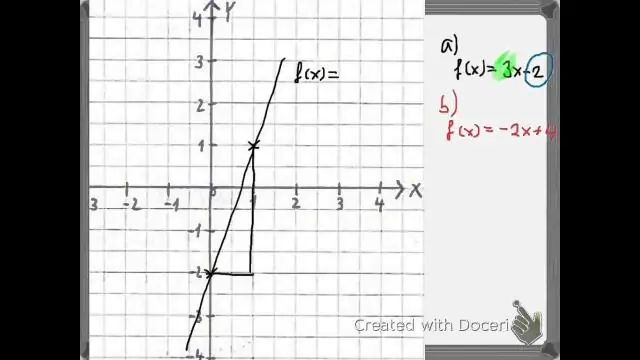
Ein … machen zusammengesetzte Funktion wobei wir g(x) in das Funktion f(x), wir können schreiben es f(g(x)). Beachten Sie, dass statt einfach ein x in die Funktion , ersetzen wir das gesamte g(x) Funktion . Wenn wir das tun, haben wir f(g(x)) = (3x) + 2. Links sehen Sie, dass das g Funktion ist innerhalb der f Funktion.
Was ist in ähnlicher Weise ein zusammengesetztes Funktionsbeispiel? EIN zusammengesetzte Funktion ist ein Funktion das hängt vom anderen ab Funktion . EIN zusammengesetzte Funktion entsteht, wenn man Funktion wird durch einen anderen ersetzt Funktion . Zum Beispiel , f(g(x)) ist der zusammengesetzte Funktion die entsteht, wenn g(x) für x in f(x) eingesetzt wird. In dem Komposition (f ο g)(x), wird der Definitionsbereich von f zu g(x).
Die Leute fragen auch, was sind die Schritte zum Lösen einer zusammengesetzten Funktion?
Hier sind die Schritte können wir verwenden, um die zu finden Komposition von zwei Funktionen : Schritt 1: Schreibe die um Komposition in anderer Form. Zum Beispiel die Komposition (f g)(x) muss in f(g(x)) umgeschrieben werden. Schritt 2: Ersetze jedes Vorkommen von x, das in der Außenseite gefunden wurde Funktion mit innen Funktion.
Was versteht man unter einer zusammengesetzten Funktion?
: ein Funktion deren Werte aus zwei gegebenen gefunden werden Funktionen indem man einen anwendet Funktion auf eine unabhängige Variable und dann Anwendung der zweiten Funktion zum Ergebnis und dessen Domäne aus den Werten der unabhängigen Variablen besteht, für die das Ergebnis der ersten Funktion liegt im Bereich des zweiten.
Empfohlen:
Wie macht man zusammengesetzte Wahrscheinlichkeitsereignisse?
Bei der Bestimmung der Wahrscheinlichkeit eines zusammengesetzten Ereignisses wird die Summe der Wahrscheinlichkeiten der einzelnen Ereignisse ermittelt und gegebenenfalls überlappende Wahrscheinlichkeiten entfernt. Ein exklusives zusammengesetztes Ereignis ist ein Ereignis, bei dem sich die mehreren Ereignisse nicht überschneiden. Mathematisch ausgedrückt: P(C) = P(A) + P(B)
Wie multipliziert man zusammengesetzte Funktionen?
Multiplikation und Zusammensetzung von Funktionen Um eine Funktion mit einem Skalar zu multiplizieren, multiplizieren Sie jede Ausgabe mit diesem Skalar. Wenn wir f (g(x)) nehmen, nehmen wir g(x) als Eingabe der Funktion f. Wenn zum Beispiel f (x) = 10x und g(x) = x + 1 sind, dann finden wir, um f (g(4)) zu finden, g(4) = 4 + 1 + 5 und berechnen dann f (5 ) = 10(5) = 50. Beispiel: f (x) = 2x - 2, g(x) = x2 - 8
Wie findet man das zusammengesetzte Wort?
Wenn zwei Wörter zusammen verwendet werden, um eine neue Bedeutung zu ergeben, wird eine Verbindung gebildet. Zusammengesetzte Wörter können auf drei Arten geschrieben werden: als offene Zusammensetzungen (als zwei Wörter geschrieben, z. zB langfristig)
Wie sieht Candida aus, wenn es aus Ihnen herauskommt?
Stuhl mit einer großen Menge an Candida kann ein weißes, faseriges Material enthalten, das wie Käsestücke aussieht. Die Candida kann auch schaumig aussehen, ähnlich wie Hefe in Brotmischung, wenn sie aufgeht. Es kann auch Schleim ähneln
Wie lautet die zusammengesetzte Formel?
Eine Verbindung ist eine Substanz, die aus einem bestimmten Verhältnis von zwei oder mehr Elementen besteht. Eine chemische Formel gibt uns die Anzahl der Atome jedes Elements in einer Verbindung an. Es enthält die Symbole der Atome der in der Verbindung vorhandenen Elemente sowie deren Anzahl für jedes Element in Form von Indizes