Video: Wie berechnet man den Verteilungskoeffizienten?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
EIN Verteilungskoeffizient ist das Verhältnis der Konzentration eines Stoffes in einem Medium oder einer Phase (C1) auf die Konzentration in einer zweiten Phase (C2) wenn die beiden Konzentrationen im Gleichgewicht sind; das ist, Verteilungskoeffizient = (C1/C2)gleich. Die Einheiten von C1 und C2 kann unterschiedlich sein.
In ähnlicher Weise kann man sich fragen, wie man den Verteilungskoeffizienten eines Arzneimittels bestimmt?
Die Verteilungskoeffizient eines Arzneimittels vielleicht bestimmt durch Schütteln mit gleichen Teilen zweier nicht mischbarer Lösungsmittel (die mit Wasser gesättigte organische Schicht und die wässrige Arzneimittel Lösung), bis das Gleichgewicht erreicht ist. Der Inhalt der Arzneimittel in einer der Schichten ist bestimmt und der Wert wird berechnet.
Was gilt außerdem als hoher Verteilungskoeffizient? … Maßeinheit namens Verteilungskoeffizient . Je größer die Löslichkeit eines Stoffes, desto höher es ist Verteilungskoeffizient , und der höher das Verteilungskoeffizient , das höher die Permeabilität der Membran für diese spezielle Substanz.
Wie ist demnach der Verteilungskoeffizient bei der Chromatographie?
Verteilungskoeffizient . Die Verteilungskoeffizient ist das Gleichgewicht Verteilung eines Analyten zwischen der Probenphase und der Gasphase. Die Proben müssen so vorbereitet werden, dass die Konzentration der flüchtigen Komponenten im Kopfraum maximiert und die unerwünschte Kontamination durch andere Verbindungen in der Probenmatrix minimiert wird.
Was ist der scheinbare Verteilungskoeffizient?
Die Scheinbare Verteilungskoeffizienten (log P,,,), wie hier berichtet, repräsentieren die Verteilung der Summen sowohl ionisierter als auch nicht ionisierter gelöster Moleküle zwischen den beiden Phasen des Testsystems.
Empfohlen:
Wie berechnet man den Umfang der Erde auf ihrem Breitengrad?
Der Umfang eines Kreises ist gleich 2&r, wobei r der Radius ist. Auf der Erde beträgt der Umfang der Kugel bei einem gegebenen Breitengrad 2&r(cos ), wobei; ist der Breitengrad und r ist der Radius der Erde am Äquator
Wie berechnet man den Potentialabfall in einer Schaltung?
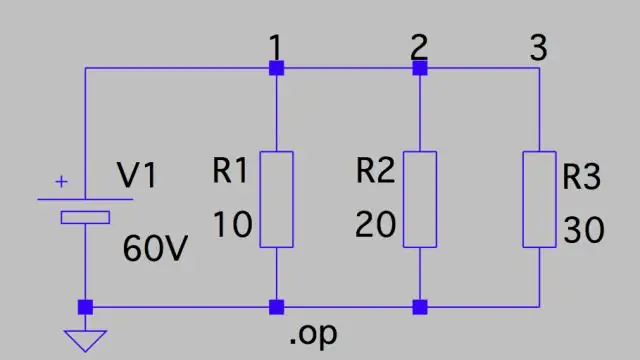
Spannungsabfall: Parallelschaltung Dies bedeutet, dass der Spannungsabfall an jedem Stromkreis nur die Gesamtspannung des Stromkreises dividiert durch die Anzahl der Widerstände im Stromkreis ist, oder 24 V/3 = 8 V
Wie berechnet man den Motorüberlaststrom?
Durch den Nenn-Volllaststrom vom Motortypenschild dividieren. Dies ist der Lastfaktor für den Motor. Wenn der Motorstrom 22 A beträgt und der Nennvolllaststrom 20 A beträgt, beträgt der Lastfaktor 22/20 = 1,1. Dadurch wird der Motor um 10 % überlastet
Wie berechnet man den Batch-Prozesszyklus?
Die Taktzeiten für im Batch-Verfahren hergestellte Artikel werden in der Regel in Zeit pro festgelegter Stückzahl, meist der Losgröße, angegeben. Bei einem Backprozess, der beispielsweise 200 Einheiten Brot auf einmal in einer Stunde backen kann, beträgt die Zykluszeit 200 Einheiten/Stunde
Welchen Einfluss hat die Temperatur auf den Verteilungskoeffizienten?
Zwischen der Temperatur und dem Verteilungskoeffizienten wurde eine inverse lineare Beziehung gefunden. Schlussfolgerung: Innerhalb eines bestimmten Temperaturbereichs nehmen die Verteilungskoeffizienten Isofluran und Sevofluran mit steigender Temperatur ab. Sevofluran weist im Vergleich zu Isofluran eine hohe Löslichkeit in Oxygent(TM) auf