Video: Wie konvertiert man die allgemeine Form in die Standardform einer Hyperbel?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
Die Standardform einer Hyperbel das sich seitwärts öffnet ist (x - h)^2 / a^2 - (y - k)^2 / b^2 = 1. Für die Hyperbel das sich nach oben und unten öffnet, es ist (y - k)^2 / a^2 - (x- h)^2 / b^2 = 1. In beiden Fällen ist das Zentrum des Hyperbel ist gegeben durch (h, k).
Außerdem, was ist die allgemeine Form einer Hyperbel?
EIN Allgemein Hinweis: Standard Formen des Gleichung einer Hyperbel mit Zentrum (0, 0) Beachten Sie, dass die Scheitelpunkte, Ko-Scheitelpunkte und Brennpunkte durch die Gleichung c2=a2+b2 c2 = a2 + b2.
Außerdem, WAS IST A in Scheitelpunktform? Die Scheitelpunktform eines Quadrats ist gegeben durch. y = a(x – h)2 + k, wobei (h, k) das ist Scheitel . Das "a" im Scheitelpunktform ist das gleiche "a" wie. in y = ax2 + bx + c (dh beide a haben genau den gleichen Wert). Das Zeichen auf "a" sagt Ihnen, ob sich das Quadrat nach oben öffnet oder nach unten öffnet.
Wie lautet hiervon die allgemeine Form einer Ellipse?
Einer Allgemeines Format von an Ellipse isax2 + von2 + cx + dy + e = 0. Aber umso nützlicher Form sieht ganz anders aus: wo der Punkt (h, k) der Mittelpunkt des Ellipse , und die Brennpunkte und die Achsenlängen der Ellipse kann aus den Werten von a undb gefunden werden.
Wie finden Sie den Scheitelpunkt in Standardform?
Scheitelpunktform der quadratischen Gleichung -MathBitsNotebook(A1 - CCSS Math) f (x) = a(x - h)2 + k, wobei (h, k) das ist Scheitel der Parabel. Zur Info: Verschiedene Lehrbücher haben unterschiedliche Interpretationen der Referenz" Standardform " einer quadratischen Funktion.
Empfohlen:
Wie konvertiert man einen Standard-Scheitelpunkt in eine faktorisierte Form?
Konvertieren zwischen verschiedenen Formen eines Quadratischen - Expii. Die Standardform ist ax^2 + bx + c. Die Scheitelpunktform ist a(x-h)^2 + k, was den Scheitelpunkt und die Symmetrieachse offenbart. Die faktorisierte Form ist a(x-r)(x-s), die die Wurzeln offenbart
Wie unterscheidet sich die Form einer Pflanzenzelle von der einer tierischen Zelle?
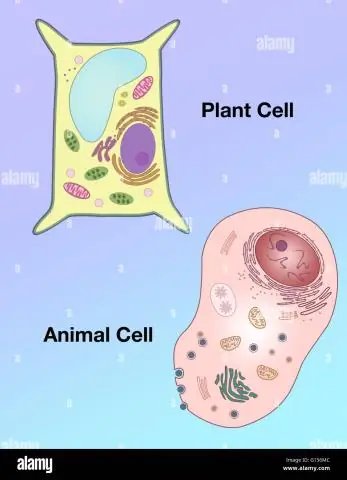
Vakuolen: Pflanzenzellen haben eine große Vakuole, während tierische Zellen mehrere kleine Vakuolen enthalten. Form: Pflanzenzellen haben eine regelmäßigere Form (im Allgemeinen rechteckig), während tierische Zellen unregelmäßige Formen haben. Lysosomen: kommen im Allgemeinen in tierischen Zellen vor, während sie in Pflanzenzellen fehlen
Was ist die Standardform der Hyperbel?
Die Standardform der Gleichung einer Hyperbel hat die Form: (x - h)^2 / a^2 - (y - k)^2 / b^2 = 1 für horizontale Hyperbeln oder (y - k)^2 / a^2 - (x - h)^2 / b^2 = 1 für vertikale Hyperbeln. Der Mittelpunkt der Hyperbel ist gegeben durch (h, k)
Wie konvertiert man eine quadratische Gleichung von der allgemeinen Form in die Standardform?
Jede quadratische Funktion kann in der Standardform f(x) = a(x - h) 2 + k geschrieben werden, wobei h und k als Koeffizienten a, b und c angegeben werden. Beginnen wir mit der quadratischen Funktion in allgemeiner Form und vervollständigen wir das Quadrat, um es in Standardform umzuschreiben
Wie findet man die Gleichung einer Hyperbel bei gegebenen Asymptoten und Brennpunkten?
Unter Verwendung der obigen Argumentation lauten die Gleichungen der Asymptoten y = ±ab(x·h) + ky = ±ab (x·h) + k. Wie Hyperbeln, die am Ursprung zentriert sind, haben Hyperbeln, die an einem Punkt (h,k) zentriert sind, Scheitelpunkte, Scheitelpunkte und Brennpunkte, die durch die Gleichung c2=a2+b2 c 2 = a 2 + b 2 . zusammenhängen