
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:32.
- Zuletzt bearbeitet 2025-01-22 16:55.
Nach Newton s Zweites Gesetz der Bewegung, auch bekannt als die Gesetz von Kraft und Beschleunigung bewirkt eine Kraft auf ein Objekt eine Beschleunigung gemäß der Formel Nettokraft = Masse x Beschleunigung. Die Beschleunigung des Objekts ist also direkt proportional zur Kraft und umgekehrt proportional zur Masse.
Anschließend kann man sich auch fragen, was ist das 2. Newtonsche Gesetz?
Newtons zweites Bewegungsgesetz bezieht sich auf das Verhalten von Objekten, für die nicht alle vorhandenen Kräfte ausgeglichen sind. Die zweites Gesetz besagt, dass die Beschleunigung eines Objekts von zwei Variablen abhängt - der auf das Objekt wirkenden Nettokraft und der Masse des Objekts.
Zweitens, wie lautet die Formel für das zweite Newtonsche Bewegungsgesetz? In Gleichung Form, Newtons zweites Bewegungsgesetz ist a = Fnetm a = F net m. Dies wird oft in der bekannteren Form geschrieben: FNetz = ma. Das Gewicht w eines Objekts ist definiert als die Schwerkraft, die auf ein Objekt der Masse m einwirkt.
Warum ist außerdem das zweite Newtonsche Gesetz wichtig?
Newtons zweites Gesetz der Bewegung F=ma ist sehr wichtig weil es den Zusammenhang zwischen Kräften und Bewegung zeigt. Es ermöglicht Ihnen, die Beschleunigung (und damit Geschwindigkeit und Position) eines Objekts mit bekannten Kräften zu berechnen. Dies ist unglaublich wertvoll für Wissenschaftler, Ingenieure, Erfinder usw.
Was ist Newtons 3-Gesetz?
Eine Kraft ist ein Stoß oder ein Zug, der auf ein Objekt als Ergebnis seiner Wechselwirkung mit einem anderen Objekt einwirkt. Diese beiden Kräfte werden Aktions- und Reaktionskräfte genannt und sind Gegenstand von Newtons drittes Gesetz der Bewegung. Formell erklärt, Newtons drittes Gesetz lautet: Für jede Aktion gibt es eine gleiche und entgegengesetzte Reaktion.
Empfohlen:
Was ist das zweite Newtonsche Gesetz in einfachen Worten?

Das zweite Newtonsche Gesetz besagt, dass die Beschleunigung eines Teilchens von den auf das Teilchen wirkenden Kräften und der Masse des Teilchens abhängt. Für ein gegebenes Teilchen wird die Beschleunigung erhöht, wenn die Nettokraft erhöht wird. Für eine gegebene Nettokraft gilt: Je mehr Masse ein Teilchen hat, desto weniger Beschleunigung hat es
Können wir das dritte Newtonsche Gesetz auf die Gravitationskraft anwenden?
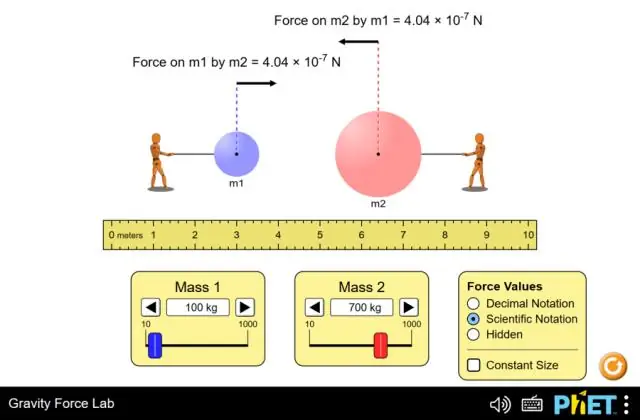
Ja, das dritte Newtonsche Gesetz gilt für die Gravitationskraft. Dies bedeutet, dass, wenn unsere Erde eine Anziehungskraft auf ein Objekt ausübt, das Objekt auch eine gleiche Kraft auf die Erde ausübt, in die entgegengesetzte Richtung. Daher können wir sagen, dass Sie das dritte Newtonsche Gesetz auf die Gravitationskraft anwenden können
Wie gilt das zweite Newtonsche Gesetz für Autos?

Der zweite Hauptsatz: Wenn auf ein Auto eine Kraft ausgeübt wird, ist die Bewegungsänderung proportional zur Kraft dividiert durch die Masse des Autos. Dieses Gesetz wird durch die berühmte Gleichung F = ma ausgedrückt, wobei F eine Kraft, m die Masse des Autos und a die Beschleunigung oder Bewegungsänderung des Autos ist
Wie wird das zweite Newtonsche Gesetz verwendet?

Zusammenfassend liefert das zweite Newtonsche Gesetz die Erklärung für das Verhalten von Objekten, bei denen die Kräfte nicht im Gleichgewicht sind. Das Gesetz besagt, dass unausgeglichene Kräfte bewirken, dass Objekte mit einer Beschleunigung beschleunigt werden, die direkt proportional zur Nettokraft und umgekehrt proportional zur Masse ist
Wie zeigt man das zweite Newtonsche Gesetz?
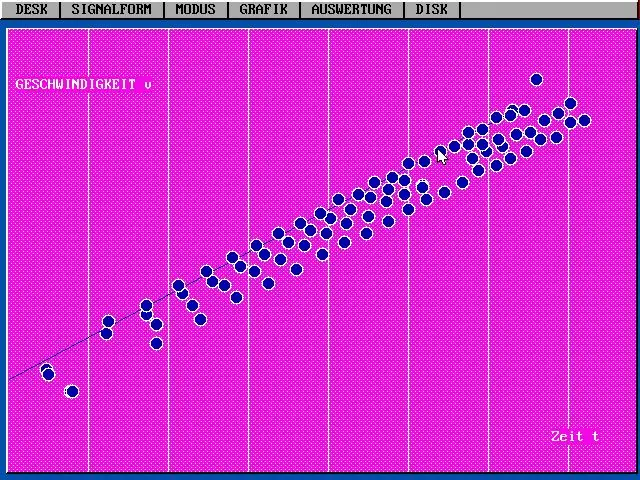
Das zweite Newtonsche Bewegungsgesetz kann formal wie folgt formuliert werden: Die Beschleunigung eines Objekts, die durch eine Nettokraft erzeugt wird, ist direkt proportional zur Größe der Nettokraft, in der gleichen Richtung wie die Nettokraft, und umgekehrt proportional zur Masse von das Objekt
