Inhaltsverzeichnis:
Video: Was ist in Mathematik und Beispielen festgelegt?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
In Mathematik , ein einstellen ist eine wohldefinierte Sammlung verschiedener Objekte, die als eigenständiges Objekt betrachtet werden. Zum Beispiel , die Zahlen 2, 4 und 6 sind getrennt betrachtet verschiedene Objekte, aber wenn sie zusammen betrachtet werden, bilden sie ein einziges einstellen der Größe drei, geschrieben {2, 4, 6}.
Was ist die Bedeutung von Menge in der Mathematik?
EIN in der mathematik setzen ist eine Sammlung wohldefinierter und unterschiedlicher Objekte, die als eigenständiges Objekt betrachtet werden. Die grundlegendsten Eigenschaften sind, dass a einstellen "hat" Elemente, und diese zwei Sätze sind nur dann gleich (ein und dasselbe), wenn jedes Element des einen Element des anderen ist.
Anschließend stellt sich die Frage, was ist in der Matheklasse 7 vorgesehen? f) Die einstellen aller Zahlen, deren Betrag gleich ist 7 . Satz A, B, C und D sind definiert durch: A ={2, 3, 4, 5, 6, 7 } B = {3, 5, 7 } C = {3, 5, 7 , 20, 25, 30}
Wissen Sie auch, was in der Mathematik mit Beispielen universell ist?
Zum Beispiel , betrachten Sie die einstelligen Zahlen 1 bis 9: Wenn {1, 2, 3, 4, 5, 6, 7, 8, 9} größer ist einstellen , dann gehören A und B dazu einstellen . Definition: A Universelles Set ist der einstellen aller Elemente unterberücksichtigt, bezeichnet mit Kapital. Alle anderen Sätze sind Teilmengen der universelles Set.
Welche Arten von Sets gibt es?
Arten von Sets
- Singleton-Set. Enthält eine Menge nur ein Element, wird sie als Singleton-Menge bezeichnet.
- Endliche Menge. Eine Menge, die aus einer natürlichen Anzahl von Objekten besteht, d. h. in der das Zahlenelement endlich ist, heißt endliche Menge.
- Unendliche Menge.
- Gleicher Satz.
- Nullmenge/ leere Menge.
- Teilmenge.
- Richtiges Set.
- Falscher Satz.
Empfohlen:
Wann wurde Maß für Maß festgelegt?
1604 Außerdem, wo findet Maß für Maß statt? Shakespeare setzte Maß für Maß in der katholischen Stadt Wien . Was bedeutet Maß für Maß? Der Titel von Maß für Maß aus der Bibel: „Richte nicht, dass du nicht gerichtet wirst. Denn mit dem Urteil, das du verkündest, wirst du gerichtet und die messen du gibst wird das sein messen du bekommst"
Was ist der Unterschied zwischen Geschwindigkeit und Geschwindigkeit mit Beispielen?
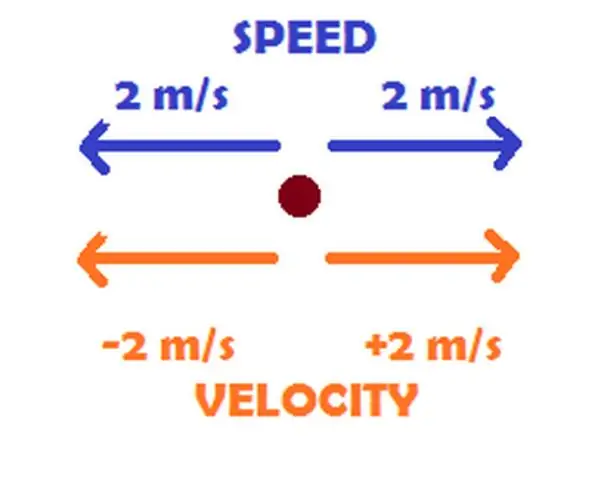
Der Grund ist einfach. Geschwindigkeit ist die Zeitgeschwindigkeit, mit der sich ein Objekt entlang eines Pfades bewegt, während Geschwindigkeit die Geschwindigkeit und Richtung der Bewegung eines Objekts ist. Zum Beispiel beschreibt 50 km/h (31 mph) die Geschwindigkeit, mit der ein Auto auf einer Straße fährt, während 50 km/h westlich die Geschwindigkeit beschreibt, mit der es fährt
Was sind die Eigenschaften von Mathematik und Beispielen?
Es gibt vier mathematische Eigenschaften, die eine Addition beinhalten. Die Eigenschaften sind die kommutativen, assoziativen, additiven Identitäts- und Distributiveigenschaften. Additive Identitätseigenschaft: Die Summe einer beliebigen Zahl und Null ist die ursprüngliche Zahl. Zum Beispiel 5 + 0 = 5
Was ist der Unterschied zwischen dichteunabhängigen und dichteabhängigen Faktoren mit Beispielen?
Es funktioniert sowohl in großen als auch in kleinen Populationen und basiert nicht auf der Bevölkerungsdichte. Dichteabhängige Faktoren sind diejenigen, die das Wachstum einer Bevölkerung in Abhängigkeit von ihrer Dichte regulieren, während dichteunabhängige Faktoren diejenigen sind, die das Bevölkerungswachstum regulieren, ohne von ihrer Dichte abhängig zu sein
Was ist physikalischer und chemischer Wandel mit Beispielen?
Eine chemische Veränderung resultiert aus einer chemischen Reaktion, während eine physikalische Veränderung besteht, wenn Materie ihre Form, aber keine chemische Identität ändert. Beispiele für chemische Veränderungen sind Brennen, Kochen, Rosten und Verrotten. Beispiele für physikalische Veränderungen sind Kochen, Schmelzen, Gefrieren und Zerkleinern