Video: Wie ermitteln Sie die Wahrscheinlichkeit, dass ein Ereignis mindestens einmal eintritt?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
Um die zu berechnen Wahrscheinlichkeit, dass ein Ereignis mindestens einmal eintritt , es wird die Ergänzung des Veranstaltung noch nie auftretend . Dies bedeutet, dass die Wahrscheinlichkeit des Veranstaltung noch nie auftretend und der Wahrscheinlichkeit des Ereignis tritt mindestens einmal auf gleich eins oder 100 % Chance.
Wie ermittelt man dann die Wahrscheinlichkeit eines Ereignisses?
Die Wahrscheinlichkeit eines Ereignisses ist die Anzahl der positiven Ergebnisse geteilt durch die Gesamtzahl der möglichen Ergebnisse. Wenn wir den Bruch 35 in eine Dezimalzahl umwandeln, würden wir sagen, dass es ein 0,6. gibt Wahrscheinlichkeit eine Banane zu wählen. Diese grundlegende Definition von Wahrscheinlichkeit geht davon aus, dass alle Ergebnisse gleich wahrscheinlich eintreten.
Anschließend stellt sich die Frage, wie hoch die Wahrscheinlichkeit ist, dass genau ein Ereignis eintritt. Zeigen Sie, dass für alle Ereignisse A und B die Wahrscheinlichkeit das genau einer von ihnen auftreten ist Pr(A) + Pr(B) − 2 Pr(A B).
Wie groß ist in Anbetracht dessen die Wahrscheinlichkeit, dass mindestens eines der drei Ereignisse eintritt?
Die Wahrscheinlichkeit, dass mindestens 1 der Ereignisse auftreten ist gleich 1 minus the Wahrscheinlichkeit dass keiner von Ereignisse auftreten . um zu sehen, ob das gut ist, nimm einfach die Möglichkeit von 1, 2 oder 3 der auftretende Ereignisse und addiere sie.
Wie groß ist die Wahrscheinlichkeit, dass mindestens einer ausfällt?
(B) Die Wahrscheinlichkeit, dass mindestens eine Komponente scheitert ist 1 minus die Wahrscheinlichkeit das gelingt alles. Seit der Wahrscheinlichkeit von einer nachfolgende Komponente ist 1 minus 0,1 oder 0,9, die Wahrscheinlichkeit dass alles erfolgreich ist (0.9)6 = 0,53 und 1–0,53 = 0,47.
Empfohlen:
Was ist ein unabhängiges Ereignis in Wahrscheinlichkeit?
Unabhängige Veranstaltungen. Wenn zwei Ereignisse als unabhängig voneinander bezeichnet werden, bedeutet dies, dass die Wahrscheinlichkeit, dass ein Ereignis eintritt, die Wahrscheinlichkeit des Eintretens des anderen Ereignisses in keiner Weise beeinflusst. Ein Beispiel für zwei unabhängige Ereignisse ist wie folgt; Sag, du hast gewürfelt und eine Münze geworfen
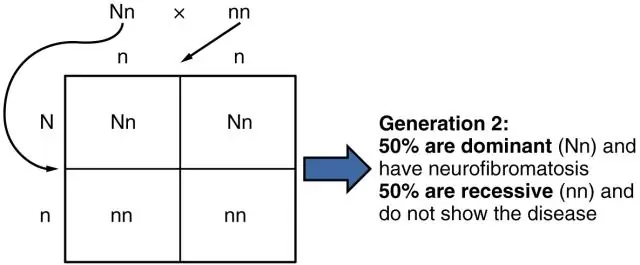
Wie hoch ist die Wahrscheinlichkeit, dass ihr Kind erkranken wird?
Wenn ein Elternteil kein Träger ist, beträgt die Wahrscheinlichkeit, dass ein Kind Träger ist, im Allgemeinen: ½ mal (die Wahrscheinlichkeit, dass der andere Elternteil Träger ist). Das heißt, wir multiplizieren die Wahrscheinlichkeit, ein Krankheitsallel zu passieren, mit der Wahrscheinlichkeit, dass der Elternteil tatsächlich das Krankheitsallel trägt
Wie groß ist die Wahrscheinlichkeit, dass eine farbenblinde Frau, die einen normalsichtigen Mann heiratet, ein farbenblindes Kind bekommt?
Wenn eine solche Trägerin mit normalem Sehvermögen (heterozygot für Farbenblindheit) einen normalen Mann (XY) heiratet, sind in der F2-Generation folgende Nachkommen zu erwarten: von den Töchtern sind 50 % normal und 50 % Träger der Krankheiten; unter den Söhnen sind 50 % farbenblind und 50 % normalsichtig
Was ist der Unterschied zwischen bedingter Wahrscheinlichkeit und gemeinsamer Wahrscheinlichkeit?
Im Allgemeinen ist die gemeinsame Wahrscheinlichkeit die Wahrscheinlichkeit, dass zwei Dinge* zusammen passieren: z. B. die Wahrscheinlichkeit, dass ich mein Auto wasche und es regnet. Bedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit, dass etwas passiert, vorausgesetzt, dass das andere passiert: z. B. die Wahrscheinlichkeit, dass es regnet, wenn ich mein Auto wasche
Wie hoch ist die Wahrscheinlichkeit, dass der Yellowstone ausbricht?
Die USGS schätzt die Wahrscheinlichkeit auf 1 zu 730.000 in einem bestimmten Jahr. Es besteht auch eine gute Chance, dass die Verschiebung der tektonischen Platten in Nordamerika die Wahrscheinlichkeit einer Eruption vollständig beseitigt hat, indem der Magma-Hotspot unter Yellowstone gezwungen wurde, auf kältere, energiefressende Gesteine zu treffen