
Inhaltsverzeichnis:
- Autor Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:32.
- Zuletzt bearbeitet 2025-01-22 16:55.
Um die Differenzidentität für Tangente zu bestimmen, verwenden Sie die Tatsache, dass tan(−β) = −tanβ
- Beispiel 1: Ermitteln Sie den genauen Wert von bräunen 75°.
- Beispiel 2: Überprüfen Sie, dass bräunen (180° − x) = − bräunen x.
- Beispiel 3: Überprüfen Sie, dass bräunen (180° + x) = bräunen x.
- Beispiel 4: Überprüfen Sie, dass bräunen (360° − x) = − bräunen x.
- Beispiel 5: Überprüfen Sie die Identität .
Außerdem, wie lautet die Formel für Tangente?
In jedem rechtwinkligen Dreieck ist die Tangente eines Winkels ist die Länge der gegenüberliegenden Seite (O) geteilt durch die Länge der benachbarten Seite (A). In einem Formel , es wird einfach als 'tan' geschrieben. Wird oft als "SOH" bezeichnet - was bedeutet, dass Sinus gegenüber der Hypotenuse steht.
Außerdem, wie schreibt man eine Tangente um? Um die Sinusfunktion in Bezug auf die Tangente umzuschreiben, gehen Sie folgendermaßen vor:
- Beginnen Sie mit der Verhältnisidentität, die Sinus, Cosinus und Tangens umfasst, und multiplizieren Sie jede Seite mit Cosinus, um den Sinus allein auf der linken Seite zu erhalten.
- Ersetze den Kosinus durch seine reziproke Funktion.
- Lösen Sie die pythagoräische Identität tan2θ + 1 = Sek.2θ für Sekante.
Wie lautet in diesem Zusammenhang die Doppelwinkelformel?
Über Transkript. Der Kosinus Doppelwinkelformel sagt uns, dass cos(2θ) immer gleich cos²θ-sin²θ ist. Zum Beispiel ist cos(60) gleich cos²(30)-sin²(30). Wir können diese Identität verwenden, um Ausdrücke umzuschreiben oder Probleme zu lösen.
Was ist die Tangentialidentität?
Die Summe Identität zum Tangente wird wie folgt abgeleitet: Zur Bestimmung der Differenz Identität zum Tangente , nutze die Tatsache, dass bräunen (−β) = −tanβ. Der Doppelwinkel Identität zum Tangente erhält man mit der Summe Identität zum Tangente . Der halbe Winkel Identität zum Tangente kann in drei verschiedenen Formen geschrieben werden.
Empfohlen:
Wie löst man eine quadratische Gleichung mit dem Nullfaktorgesetz?

Daraus können wir folgern: Wenn das Produkt zweier Zahlen Null ist, dann ist eine oder beide Zahlen Null. Das heißt, wenn ab = 0, dann ist a = 0 oder b = 0 (was die Möglichkeit einschließt, dass a = b = 0 ist). Dies wird als Nullfaktorgesetz bezeichnet; und wir verwenden es oft, um quadratische Gleichungen zu lösen
Wie löst man einen Bremssattelkolben?

Um einen festsitzenden Bremssattelkolben zu entfernen, kann der Hydraulikdruck der Bremsanlage selbst genutzt werden. Entfernen Sie den Bremssattel von der Bremsscheibe und pumpen Sie das Bremspedal, um den Kolben über den korrodierten Teil hinaus zu bewegen. Jetzt solltest du es zerlegen und wieder aufbauen können
Wie löst man Hardy-Weinberg-Probleme?

VIDEO Wie findet man außerdem P und Q in Hardy Weinberg? Schon seit P = 1 - Q und Q bekannt ist, ist es möglich p berechnen sowie. Wissen p und q , ist es einfach, diese Werte in die Winterhart - Weinberg Gleichung (p² + 2pq + q² = 1).
Wie löst man den Koeffizienten, indem man das Quadrat vervollständigt?

Nun können wir eine quadratische Gleichung in 5 Schritten lösen: Schritt 1 Dividiere alle Terme durch a (den Koeffizienten von x2). Schritt 2 Verschieben Sie den Zahlenterm (c/a) auf die rechte Seite der Gleichung. Schritt 3 Vervollständigen Sie das Quadrat auf der linken Seite der Gleichung und gleichen Sie dies aus, indem Sie den gleichen Wert zur rechten Seite der Gleichung hinzufügen
Wie löst man eine Gleichung, indem man die Variable isoliert?
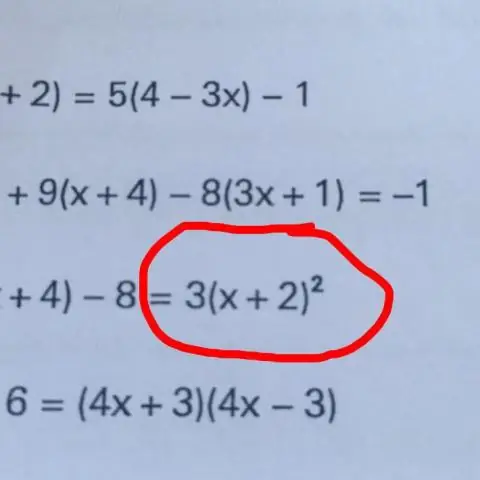
Die grundlegende Technik, eine Variable zu isolieren, besteht darin, „etwas auf beiden Seiten der Gleichung zu tun“, wie zum Beispiel Addieren, Subtrahieren, Multiplizieren oder Dividieren beider Seiten der Gleichung durch dieselbe Zahl. Durch Wiederholen dieses Vorgangs können wir die Variable auf einer Seite der Gleichung isoliert bekommen
