Inhaltsverzeichnis:
- Autor Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:32.
- Zuletzt bearbeitet 2025-01-22 16:55.
Die Quadrat Wurzel Funktion ist eins zu eins Funktion das nimmt eine nicht negative Zahl als Eingabe und gibt die zurück Quadrat Wurzel dieser Zahl als Ausgabe. Zum Beispiel wird die Zahl 9 auf die Zahl 3 abgebildet quadratische Funktion nimmt eine beliebige Zahl (positiv oder negativ) als Eingabe und gibt die zurück Quadrat dieser Zahl als Ausgabe.
Die Frage ist auch, wie findet man das Quadrat einer Funktion?
Schritte
- Schritt 1 Dividiere alle Terme durch a (der Koeffizient von x2).
- Schritt 2 Verschieben Sie den Zahlenterm (c/a) auf die rechte Seite der Gleichung.
- Schritt 3 Vervollständigen Sie das Quadrat auf der linken Seite der Gleichung und gleichen Sie dies aus, indem Sie den gleichen Wert auf der rechten Seite der Gleichung hinzufügen.
Außerdem, warum quadrieren wir eine Zahl? In einer Nussschale, wir quadrieren negativ bleiben Zahlen vom stinkenden Chaos. Da ein Negativ eher eine Richtung als einen Wert bedeuten kann, d. h. links vs. rechts oder abwärts vs. oben, ist es nützlich, kontinuierlich von einem Punkt zum anderen zu gehen, ohne dass "Negative" die Entfernung aufheben.
Auch zu wissen, wie man einen Bruch quadriert?
Zu einen Bruch quadrieren , vereinfachen die Fraktion so viel wie du kannst. Als nächstes multiplizieren Sie den Zähler mit sich selbst und dann den Nenner mit sich selbst. Wenn Sie ein Negativ quadrieren Fraktion , das Ergebnis ist positiv. Reduzieren Sie die Fraktion zu seiner einfachsten Form.
Ist ein Quadrat eine Funktion?
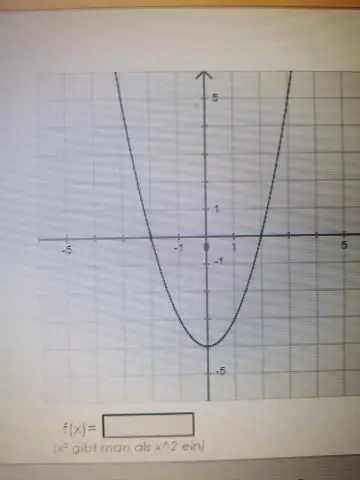
Die Quadrat einer Zahl ist die Zahl mit sich selbst multipliziert. EIN quadratische Funktion ist eine quadratische Funktion . Sein Elternteil Funktion ist y=x^2 und sein Graph ist eine Parabel. EIN Quadrat Wurzel Funktion ist ein Funktion mit den Eltern Funktion y=Quadrat{x}.
Empfohlen:
Wie stellt man fest, ob eine Funktion eine horizontale Tangente hat?

Horizontale Linien haben eine Steigung von Null. Wenn die Ableitung null ist, ist die Tangente daher horizontal. Um horizontale Tangenten zu finden, verwenden Sie die Ableitung der Funktion, um die Nullstellen zu lokalisieren und sie wieder in die ursprüngliche Gleichung einzufügen
Wie stellt man fest, ob eine Relation eine Funktion in einem Graphen ist?

ANTWORT: Beispielantwort: Sie können feststellen, ob jedes Element der Domäne mit genau einem Element des Bereichs gepaart ist. Wenn Sie beispielsweise ein Diagramm erhalten, können Sie den vertikalen Linientest verwenden; Wenn eine vertikale Linie den Graphen mehr als einmal schneidet, dann ist die Beziehung, die der Graph darstellt, keine Funktion
Wie erkennt man, ob eine Funktion keine Funktion ist?

Die Bestimmung, ob eine Relation eine Funktion in einem Graphen ist, ist mit Hilfe des vertikalen Linientests relativ einfach. Wenn eine senkrechte Linie die Relation im Graphen nur einmal an allen Stellen schneidet, ist die Relation eine Funktion. Wenn jedoch eine vertikale Linie die Relation mehr als einmal schneidet, ist die Relation keine Funktion
Wie ändert man eine Funktion in eine Scheitelpunktform?

Um eine quadratische Form von y = ax2 + bx + c in eine Scheitelpunktform umzuwandeln, y = a(x - h)2+ k, verwenden Sie den Prozess der Vervollständigung des Quadrats. Sehen wir uns ein Beispiel an. Wandeln Sie y = 2x2 - 4x + 5 in die Scheitelpunktform um und geben Sie den Scheitelpunkt an. Gleichung in y = ax2 + bx + c-Form
Wie erkennt man, ob eine Funktion eine Potenzfunktion ist?

VIDEO Ebenso fragen die Leute, was eine Funktion zu einer Potenzfunktion macht? EIN Power-Funktion ist ein Funktion wobei y = x ^n wobei n eine beliebige reelle konstante Zahl ist. Viele unserer Eltern Funktionen wie linear Funktionen und quadratisch Funktionen sind in der Tat Leistungsfunktionen .
