Inhaltsverzeichnis:
Video: Wie finden Sie den Scheitelpunkt und die Directrix?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
Die Standardform ist (x - h)2 = 4p (y - k), wobei der Fokus (h, k + p) ist und die Direktion ist y = k - p. Wenn die Parabel so gedreht wird, dass sie Scheitel (h, k) ist und seine Symmetrieachse parallel zur x-Achse ist, hat es eine Gleichung von (y - k)2 = 4p (x - h), wobei der Fokus (h + p, k) ist und die Direktion ist x = h - p.
Wie findet man ähnlich die Scheitelpunktform einer Parabel?
f(x) = a(x - h)2 + k, wobei (h, k) das ist Scheitel des Parabel . Zu Ihrer Information: Verschiedene Lehrbücher haben unterschiedliche Interpretationen der Referenz "Standard". Form " einer quadratischen Funktion. Manche sagen f (x) = ax2 + bx + c ist "Standard" Form ", während andere sagen, dass f (x) = a(x - h)2 + k ist "Standard" Form ".
Man kann sich auch fragen, wie schreibt man eine Gleichung für eine Parabel? Zum Parabeln die sich entweder nach oben oder unten öffnen, die Standardform Gleichung ist (x - h)^2 = 4p(y - k). Zum Parabeln die sich seitlich öffnen, die Standardform Gleichung ist (y - k)^2 = 4p(x - h). Der Scheitel oder die Spitze unserer Parabel ist durch den Punkt (h, k) gegeben.
Man kann sich auch fragen, wie findet man den Scheitelpunkt?
Schritte zum Lösen
- Erhalten Sie die Gleichung in der Form y = ax2 + bx + c.
- Berechnen Sie -b / 2a. Dies ist die x-Koordinate des Scheitelpunkts.
- Um die y-Koordinate des Scheitelpunkts zu finden, setzen Sie einfach den Wert von -b / 2a in die Gleichung für x ein und lösen Sie nach y auf. Dies ist die y-Koordinate des Scheitelpunkts.
Was ist P in einer Parabel?
EIN Parabel ist die Ansammlung von Punkten in der Ebene, die von F und d gleich weit entfernt sind. Der Punkt F heißt Fokus und die Linie d heißt Leitlinie. Der Punkt P ist ein typischer Punkt auf dem Parabel so dass sein Abstand von der Leitlinie, PQ, gleich seinem Abstand von F, PF ist.
Empfohlen:
Wie finden Sie die Bogenlänge und die Sektorfläche?
Ein Zentriwinkel, der von einem großen Bogen begrenzt wird, hat ein Maß größer als 180°. Die Bogenlängenformel wird verwendet, um die Länge eines Kreisbogens zu ermitteln; l = r&thgr; l = r&thgr;, wobei &thgr; ist im Bogenmaß. Sektorbereich wird gefunden: A = 12&r2 A = 1 2 &; r 2, wobei &thgr; ist im Bogenmaß
Wie viele Valenzelektronen finden sich in den Halogenen, den Alkalimetallen und den Erdalkalimetallen?
Die Halogene haben alle die allgemeine Elektronenkonfiguration ns2np5, was ihnen sieben Valenzelektronen verleiht. Sie haben ein Elektron weniger als die vollen äußeren s- und p-Unterniveaus, was sie sehr reaktiv macht. Besonders heftig reagieren sie mit den reaktiven Alkalimetallen
Wie beschriftet man den Scheitelpunkt und die Symmetrieachse?
Die Symmetrieachse geht immer durch den Scheitel der Parabel. Die x-Koordinate des Scheitelpunkts ist die Gleichung der Symmetrieachse der Parabel. Für eine quadratische Funktion in Standardform, y=ax2+bx+c, ist die Symmetrieachse eine vertikale Linie x=−b2a
Wie finden Sie den Mittelwert und den Median im Tableau?
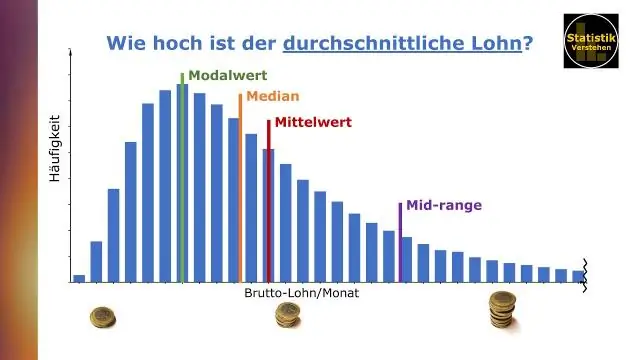
Kommunizieren von Daten mit Tableau von Ben Jones Der Mittelwert (oder Durchschnitt) wird durch Summieren aller Werte in einem Datensatz und Dividieren durch die Anzahl der Werte bestimmt. Der Median ist der Mittelwert in einem Datensatz, in dem die Werte größenordnungsmäßig eingeordnet sind
Wie findet man den Scheitelpunkt einer horizontalen Parabel?
Wenn eine Parabel eine horizontale Achse hat, ist die Standardform der Gleichung der Parabel diese: (y - k) 2 = 4p(x - h), wobei p'ne; 0. Der Scheitelpunkt dieser Parabel liegt bei (h, k). Der Fokus liegt bei (h + p, k). Thedirectrix ist die Linie x = h - p