- Autor Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:32.
- Zuletzt bearbeitet 2025-01-22 16:55.
Logarithmische Funktionen sind die Umkehrungen von Exponentialfunktionen . Das Gegenteil von Exponentialfunktion y = ax ist x = aja. Die logarithmische Funktion y = logeinx ist definiert als äquivalent zu exponentiell Gleichung x = aja. y = logeinx nur unter folgenden Bedingungen: x = aja, a > 0 und a≠1.
Was ist dementsprechend der Unterschied zwischen Exponential- und Logarithmusfunktionen?
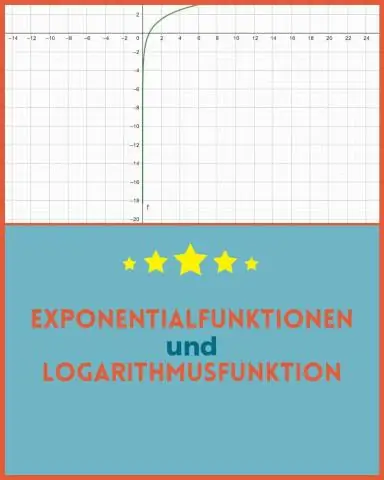
Die Umkehrung von an Exponentialfunktion ist ein logarithmische Funktion und die Umkehrung von a logarithmische Funktion ist ein Exponentialfunktion . Beachten Sie auch in der Grafik, dass mit zunehmender x-Größe die Funktion Der Wert von f(x) nimmt immer dramatischer zu.
Was ist ein Beispiel für eine logarithmische Funktion? EIN Logarithmus ist ein Exponent. Jeder exponentielle Ausdruck kann umgeschrieben werden in logarithmisch Form. Zum Beispiel , wenn wir 8 = 23 haben, dann ist die Basis 2, der Exponent ist 3 und das Ergebnis ist 8. Dies kann umgeschrieben werden in logarithmisch bilden als. 3 = Protokoll 2 8.
Was ist in diesem Zusammenhang exponentieller Logarithmus?
Per Definition: Protokoll By = x bedeutet b x = j. Passend zu jedem Logarithmus Funktion mit der Basis b sehen wir, dass es an exponentiell Funktion mit Basis b: y = b x. Ein exponentiell Funktion ist die Umkehrung von a Logarithmus Funktion.
Was ist ein Beispiel für eine Exponentialfunktion?
In einem (n Exponentialfunktion , die unabhängige Variable oder der x-Wert ist der Exponent , während die Basis eine Konstante ist. Zum Beispiel , y = 2x wäre an Exponentialfunktion . So sieht das aus. Die Formel für an Exponentialfunktion ist y = abx, wobei a und b Konstanten sind.
Empfohlen:
Welche Gezeiten sind wirklich hoch und treten zweimal im Monat auf, wenn Mond und Sonne ausgerichtet sind?

Der Begriff leitet sich vielmehr von dem Konzept der Flut ab, die „hervorspringt“. Springfluten treten das ganze Jahr über zweimal pro Mondmonat auf, unabhängig von der Jahreszeit. Nipptiden, die ebenfalls zweimal im Monat auftreten, treten auf, wenn Sonne und Mond im rechten Winkel zueinander stehen
Inwiefern ähneln sich Exponential- und Logistikfunktionen?

Exponentielles Bevölkerungswachstum: Wenn die Ressourcen unbegrenzt sind, weisen die Bevölkerungen ein exponentielles Wachstum auf, was zu einer J-förmigen Kurve führt. Wenn die Ressourcen begrenzt sind, zeigt die Bevölkerung ein logistisches Wachstum. Beim logistischen Wachstum nimmt die Bevölkerungsexpansion ab, da die Ressourcen knapp werden
Was sind die fünf Schritte, die an der extrazellulären Zellsignalisierung beteiligt sind?

Die Kommunikation durch extrazelluläre Signale umfasst normalerweise sechs Schritte: (1) Synthese und (2) Freisetzung des Signalmoleküls durch die Signalzelle; (3) Transport des Signals zur Zielzelle; (4) Nachweis des Signals durch ein spezifisches Rezeptorprotein; (5) eine Veränderung des Zellstoffwechsels, der Zellfunktion oder der Entwicklung
Was sind die Nullstellen der Funktion Was sind die Multiplizitäten?

Die Häufigkeit, mit der ein bestimmter Faktor in der faktorisierten Form der Gleichung eines Polynoms vorkommt, wird als Multiplizität bezeichnet. Die diesem Faktor zugeordnete Null, x = 2, hat die Multiplizität 2, da der Faktor (x'2) zweimal auftritt. Der x-Achsenabschnitt x=−1 ist die wiederholte Lösung des Faktors (x+1)3=0 (x + 1) 3 = 0
Was sind die fünf grundlegenden Schaltungskomponenten, was sind ihre Einheit?

Dies sind die häufigsten Komponenten: Widerstände. Kondensatoren. LEDs. Transistoren. Induktoren. Integrierte Schaltkreise
