Inhaltsverzeichnis:
Video: Wie findet man mit Pythagoras die gegenüberliegende Seite eines Dreiecks?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
Rechte Dreiecke und der Satz des Pythagoras
- Die Pythagoräer Satz, a2+b2=c2, a 2 + b 2 = c 2, kann verwendet werden, um die Länge von any Seite von einem Recht Dreieck .
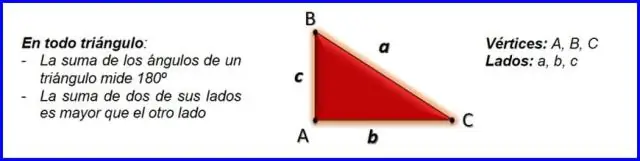
- Die gegenüberliegende Seite der rechte Winkel heißt Hypotenuse ( Seite c in der Abbildung).
Wie findet man hier die gegenüberliegende Seite eines Dreiecks?
Um herauszufinden welche, benennen wir zuerst die Seiten:
- Angrenzend ist angrenzend (neben) an den Winkel,
- Gegenüber ist der Winkel,
- und die längste Seite ist die Hypotenuse.
Ebenso, was ist eine Dreiecksformel? Die Dreiecksformel sind unten angegeben als, Umfang von a Dreieck = a + b + c. Bereich; von; ein; Dreieck = frak{1}{2}bh. Dabei ist b die Basis von Dreieck . h ist die Höhe des Dreieck.
Ähnlich kann man fragen, wie findet man die fehlende Seite eines Dreiecks mit einer Seite und einem Winkel?
Satz des Pythagoras (Theorem des Pythagoras) Die Hypotenuse ist die längste Seite von einem Recht Dreieck , und befindet sich gegenüber der rechten Winkel . Also, wenn du die Längen von zwei kennst Seiten , alles, was Sie tun müssen, ist die beiden Längen zu quadrieren, das Ergebnis zu addieren und dann die Quadratwurzel der Summe zu ziehen, um die Länge der Hypotenuse zu erhalten.
Wie findet man die fehlende Seite eines gleichschenkligen Dreiecks?
Zu finden ein Unbekannter Seite von a Dreieck , Sie müssen die Länge der anderen beiden kennen Seiten und/oder die Höhe. Zu finden die unbekannte Basis von an gleichschenkligen Dreiecks , unter Verwendung der folgenden Formel : 2 * sqrt(L^2 - A^2), wobei L die Länge der anderen beiden Schenkel und A die Höhe der Dreieck.
Empfohlen:
Wie findet man den Kosinuswert eines Dreiecks?
In jedem rechtwinkligen Dreieck ist der Kosinus eines Winkels die Länge der angrenzenden Seite (A) geteilt durch die Länge der Hypotenuse (H). In einer Formel wird es einfach als 'cos' geschrieben. Wird oft als "CAH" bezeichnet - was bedeutet, dass Cosinus über Hypotenuse benachbart ist
Wie findet man Median und Schwerpunkt eines Dreiecks?
Um den Schwerpunkt eines Dreiecks zu lokalisieren, ist es am einfachsten, alle drei Mediane zu zeichnen und nach ihrem Schnittpunkt zu suchen. Um den Median eines Dreiecks zu zeichnen, suchen Sie zuerst den Mittelpunkt einer Seite des Dreiecks. Zeichnen Sie ein Liniensegment, das diesen Punkt mit dem gegenüberliegenden Scheitelpunkt verbindet
Wie findet man die Diagonale eines rechtwinkligen Dreiecks?
Um die Länge der Diagonale (Orhypotenuse) eines rechtwinkligen Dreiecks zu ermitteln, setzen Sie die Längen der beiden senkrechten Seiten in die Formel a2 + b2 = c2 ein, wobei a und b die Längen der senkrechten Seiten und c die Länge der Hypotenuse sind
Wie beweist man, dass die Summe der Außenwinkel eines Dreiecks 360 beträgt?
Ein Außenwinkel eines Dreiecks ist gleich der Summe der gegenüberliegenden Innenwinkel. Für mehr dazu siehe Außenwinkelsatz des Dreiecks. Wenn an jedem Scheitelpunkt der äquivalente Winkel genommen wird, addieren sich die Außenwinkel immer zu 360°. Tatsächlich gilt dies für jedes konvexe Polygon, nicht nur für Dreiecke
Warum muss das Orthozentrum eines stumpfen Dreiecks auf der Außenseite des Dreiecks liegen?
Es stellt sich heraus, dass sich alle drei Höhen immer im selben Punkt schneiden – dem sogenannten Orthozentrum des Dreiecks. Das Orthozentrum liegt nicht immer innerhalb des Dreiecks. Wenn das Dreieck stumpf ist, liegt es außerhalb. Dazu müssen die Höhenlinien so verlängert werden, dass sie sich kreuzen