
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:32.
- Zuletzt bearbeitet 2025-01-22 16:55.
Da k konstant ist (für jeden Punkt gleich), können wir k an einem beliebigen Punkt finden, indem wir die y-Koordinate durch die x-Koordinate dividieren. Wenn beispielsweise y direkt als x variiert und y = 6 ist, wenn x = 2, ist die Konstante von Variation ist k = = 3. Somit ist die Gleichung das beschreiben direkte Variation ist y = 3x.
Was ist außerdem eine direkte Variationsgleichung?
Definition von direkte Variation . 1: mathematische Beziehung zwischen zwei Variablen, die durch an. ausgedrückt werden kann Gleichung wobei eine Variable gleich einer Konstanten mal der anderen ist. 2: ein Gleichung oder Funktion ausdrücken direkte Variation - invers vergleichen Variation.
Zweitens, was sind die Beispiele für direkte Variation? Etwas Beispiele für direkte Variation Probleme im wirklichen Leben: Die Anzahl der Arbeitsstunden und die Höhe Ihres Gehaltsschecks. Das Gewicht einer Feder und die Strecke, die die Feder dehnt.
Beispiel:
- die Gleichung, die x und y verbindet.
- der Wert von y, wenn x = 15.
- der Wert von x, wenn y = 6.
Was ist demnach eine Variationsgleichung?
In dem Gleichung y = mx + b, wenn m eine von Null verschiedene Konstante und b = 0 ist, dann haben Sie die Funktion y = mx (oft geschrieben y = kx), die als direkt bezeichnet wird Variation . Das heißt, Sie können sagen, dass Sie variiert direkt, da x oder y direkt proportional zu x ist.
Was ist ein direkter Variationsgraph?
EIN Graph zeigt an direkte Variation wenn es durch den Ursprung geht, (0, 0). Die Gleichung lautet y=kx, wobei k eine Konstante ist, was offensichtlich wird, wenn wir die Gleichung als yx=k schreiben. In der Form der Steigung und des Achsenabschnitts wäre die Gleichung y=mx+b, wobei m=k und b=0 sind.
Empfohlen:
Wie schreibt man die Formel für eine Verbindung, die ein mehratomiges Ion enthält?
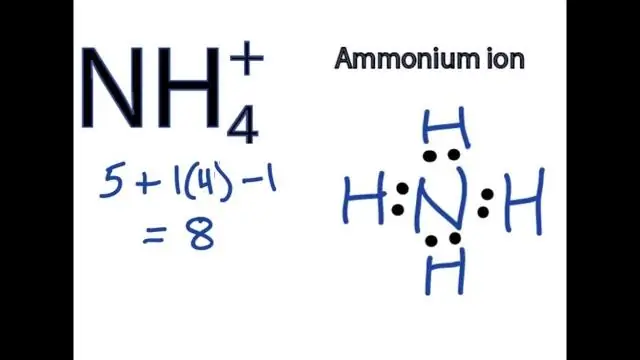
Um Formeln für Verbindungen mit mehratomigen Ionen zu schreiben, schreiben Sie das Symbol für das Metallion gefolgt von der Formel für das mehratomige Ion und gleichen Sie die Ladungen aus. Um eine Verbindung mit einem mehratomigen Ion zu benennen, geben Sie zuerst das Kation und dann das Anion an
Wie schreibt man eine Gleichung in Punktsteigungsform bei zwei Punkten?

Es gibt verschiedene Formen, in denen wir die Gleichung einer Geraden schreiben können: die Punkt-Steigungs-Form, die Steigungs-Achsen-Form, die Standardform usw. Die Gleichung einer Geraden gegeben zwei Punkte (x1, y1) und (x2, y2 ) durch die die Linie geht ist gegeben durch ((y - y1)/(x - x1)) / ((y2 - y1)/(x2 - x1))
Wie schreibt man eine Koordinatenregel für eine Drehung?

Um eine Regel für diese Rotation zu schreiben, würdest du schreiben: R270? (x,y) = (−y,x). Notationsregel Eine Notationsregel hat die Form R180? A → O = R180? (x,y) → (−x,−y) und teilt Ihnen mit, dass das Bild A um den Ursprung gedreht wurde und sowohl die x- als auch die y-Koordinaten mit -1 . multipliziert werden
Wie schreibt man eine Funktionsregel für eine Eingabe-Ausgabe-Tabelle?
Jedes Zahlenpaar in der Tabelle ist durch dieselbe Funktionsregel verbunden. Diese Regel lautet: Multiplizieren Sie jede Eingabenummer (egin{align*}xend{align*}-Wert) mit 3, um die Ausgabenummer (egin{align*}yend{align*}-Wert) zu finden. Sie können eine solche Regel verwenden, um auch andere Werte für diese Funktion zu finden
Wie schreibt man eine Gleichung in Form eines Steigungsabschnitts für eine Tabelle?
Nehmen Sie die Gleichung y = mx + b und setzen Sie den m-Wert (m = 1) und ein Paar von (x, y)-Koordinaten aus der Tabelle ein, z. B. (5, 3). Dann nach b auflösen. Verwenden Sie schließlich die gefundenen m- und b-Werte (m = 1 und b = -2), um die Gleichung zu schreiben
