Inhaltsverzeichnis:
Video: Wie schreibt man eine Gleichung in Punktsteigungsform bei zwei Punkten?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
Es gibt verschiedene Formen was wir können schreiben das Gleichung einer Linie: die Punkt - Hangform , das Neigung -abfangen Form , Der Standard Form , usw. Die Gleichung einer Linie zwei Punkte vergeben (x1, y1) und (x2, y2) durch die die Gerade verläuft ist gegeben durch ((y – y1)/(x – x1))/((y2 – y1)/(x2 – x1)).
Außerdem, wie schreibt man die Gleichung einer Geraden mit zwei Punkten?
Finden Sie die Gleichung einer gegebenen Geraden Dass Sie wissen Zwei Punkte es geht durch. Die Geradengleichung wird typischerweise als y=mx+b geschrieben, wobei m die Steigung und b der y-Achsenabschnitt ist.
Was ist außerdem die Definition der Punktsteigungsform? Definition von Punkt - Hangform .: die Gleichung einer Geraden im Form y − y1 = m(x − x1) wobei m das ist Neigung der Linie und (x1, ja1) sind die Koordinaten einer gegebenen Punkt auf der Linie - vergleichen Neigung -abfangen Form.
Wie finden Sie in Anbetracht dessen die Steigung bei zwei Punkten?
Es gibt drei Schritte, um die Steigung einer geraden Linie zu berechnen, wenn Sie ihre Gleichung nicht erhalten
- Schritt 1: Identifizieren Sie zwei Punkte auf der Linie.
- Schritt zwei: Wählen Sie eines als (x1, y1) und das andere als (x2, y2) aus.
- Schritt 3: Verwenden Sie die Steigungsgleichung, um die Steigung zu berechnen.
Was ist die Y-Intercept-Form?
In der Gleichung einer geraden Linie (wenn die Gleichung geschrieben wird als " ja = mx + b"), die Steigung ist die Zahl "m", die mit x multipliziert wird, und "b" ist die ja - abfangen (d. h. der Punkt, an dem die Linie die Vertikale schneidet ja -Achse). Dieses nützliche Form der Liniengleichung wird sinnvollerweise als "Steigungs- abfangen ".
Empfohlen:
Wie findet man die Komponentenform von zwei Punkten?
Gegeben sind zwei Punktvektoren, von denen einer den Anfangspunkt und der andere den Endpunkt darstellt. Die Komponentenform des durch die beiden Punktvektoren gebildeten Vektors ergibt sich aus den Komponenten des Endpunktes minus den entsprechenden Komponenten des Anfangspunktes
Wie schreibt man eine quadratische Gleichung in C++?
Programm 2: finde a b und c in einer quadratischen Gleichung #include #include int main(){float a,b,c; float d,root1,root2; printf('Quadratische Gleichung im Format ax^2+bx+c eingeben: '); scanf('%fx^2%fx%f',&a,&b,&c); d = b * b - 4 * a * c;
Wie findet man den Abstand zwischen zwei Punkten in einem Graphen?
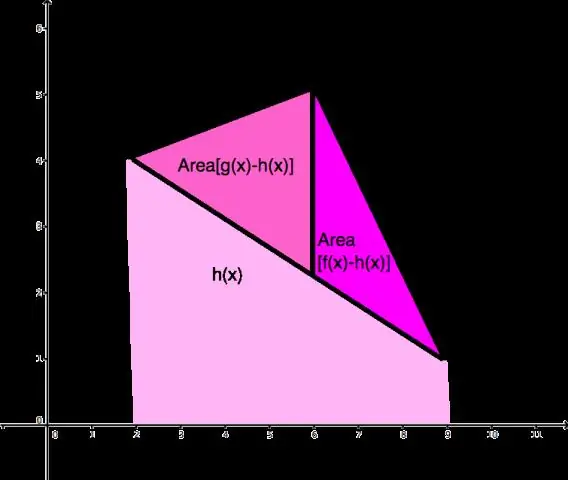
Schritte Nehmen Sie die Koordinaten von zwei Punkten, zwischen denen Sie den Abstand ermitteln möchten. Nennen Sie einen Punkt Punkt 1(x1,y1) und machen Sie den anderen Punkt 2 (x2,y2). Kenne die Distanzformel. Ermitteln Sie den horizontalen und vertikalen Abstand zwischen den Punkten. Beide Werte quadrieren. Addiere die quadrierten Werte zusammen. Ziehe die Quadratwurzel der Gleichung
Wie stellt man eine Gleichung mit zwei Punkten auf?
Gleichung aus 2 Punkten mit Slope Intercept Form Berechnen Sie die Steigung aus 2 Punkten. Setze einen der Punkte in die Gleichung ein. Sie können entweder (3,7) oder (5,11) verwenden. Auflösen nach b, dem y-Achsenabschnitt der Geraden. Setze b, -1, in die Gleichung aus Schritt 2 ein
Wie schreibt man eine Gleichung in Form eines Steigungsabschnitts für eine Tabelle?
Nehmen Sie die Gleichung y = mx + b und setzen Sie den m-Wert (m = 1) und ein Paar von (x, y)-Koordinaten aus der Tabelle ein, z. B. (5, 3). Dann nach b auflösen. Verwenden Sie schließlich die gefundenen m- und b-Werte (m = 1 und b = -2), um die Gleichung zu schreiben