Video: Was ist die Directrix in einer Parabel?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
Directrix . EIN Parabel ist die Menge aller Punkte in einer Ebene, die von einem bestimmten Punkt und einer bestimmten Linie gleich weit entfernt sind. Der Punkt wird als Brennpunkt bezeichnet Parabel , und die Linie heißt die Direktion . Die Direktion steht senkrecht zur Symmetrieachse von a Parabel und berührt nicht die Parabel.
Außerdem, wie findet man die Directrix einer Parabel?
Die Standardform ist (x - h)2 = 4p (y - k), wobei der Fokus (h, k + p) ist und die Direktion ist y = k - p. Wenn die Parabel so gedreht wird, dass sein Scheitel (h, k) ist und seine Symmetrieachse parallel zur x-Achse ist, hat es eine Gleichung von (y - k)2 = 4p (x - h), wobei der Fokus (h + p, k) ist und die Direktion ist x = h - p.
Und wie findet man die Scheitelpunktform einer Parabel? f(x) = a(x - h)2 + k, wobei (h, k) das ist Scheitel des Parabel . Zu Ihrer Information: Verschiedene Lehrbücher haben unterschiedliche Interpretationen der Referenz "Standard". Form " einer quadratischen Funktion. Manche sagen f (x) = ax2 + bx + c ist "Standard" Form ", während andere sagen, dass f (x) = a(x - h)2 + k ist "Standard" Form ".
Ähnlich kann man fragen, was ist die Directrix einer Hyperbel?
Im Fall von a Hyperbel , ein Direktion ist eine Gerade, bei der der Abstand von jedem Punkt auf der Hyperbel zu einem seiner beiden Brennpunkte ist mal der senkrechte Abstand von zum Direktion , wobei eine Konstante größer als ist. Beachten Sie, dass Hyperbeln haben zwei Brennpunkte und zwei Direktionen, eine für jeden Brennpunkt.
Wie findet man die Directrix einer Gleichung?
Die Standardform ist (x - h)2 = 4p (y - k), wobei der Fokus (h, k + p) ist und die Direktion ist y = k - p. Wenn die Parabel so gedreht wird, dass ihr Scheitel (h, k) und ihre Symmetrieachse parallel zur x-Achse ist, hat sie an Gleichung von (y - k)2 = 4p (x - h), wobei der Fokus (h + p, k) ist und die Direktion ist x = h - p.
Empfohlen:
Was ist der Unterschied zwischen einer zytoplasmatischen Reaktion und einer nuklearen Reaktion?
Was ist der Unterschied zwischen einer nuklearen Reaktion und einer zytoplasmatischen Reaktion? Eine nukleäre Reaktion beinhaltet die Veränderung der Genexpression, während eine zytoplasmatische Reaktion die Aktivierung eines Enzyms oder die Öffnung eines Ionenkanals beinhaltet
Was ist der maximale oder minimale Punkt einer Parabel?
Vertikale Parabeln geben eine wichtige Information: Wenn sich die Parabel öffnet, ist der Scheitelpunkt der tiefste Punkt auf dem Graphen – Minimum oder Min genannt. Wenn sich die Parabel nach unten öffnet, ist der Scheitelpunkt der höchste Punkt im Graphen – genannt das Maximum oder max
Wie zeichnet man einen Kegelschnitt einer Parabel?
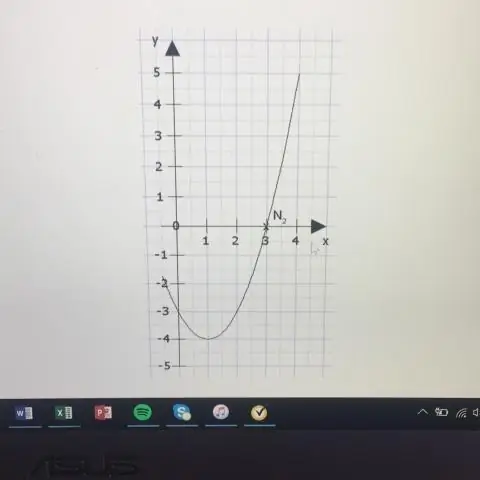
Die Leitlinie ist die Linie y = k - p. Die Achse ist die Linie x = h. Wenn p > 0, öffnet sich die Parabel nach oben, und wenn p < 0, öffnet sich die Parabel nach unten. Wenn eine Parabel eine horizontale Achse hat, ist die Standardform der Gleichung der Parabel diese: (y - k)2 = 4p(x - h), wobei p≠ 0
Wie findet man den Scheitelpunkt einer horizontalen Parabel?
Wenn eine Parabel eine horizontale Achse hat, ist die Standardform der Gleichung der Parabel diese: (y - k) 2 = 4p(x - h), wobei p'ne; 0. Der Scheitelpunkt dieser Parabel liegt bei (h, k). Der Fokus liegt bei (h + p, k). Thedirectrix ist die Linie x = h - p
Wie macht man einen Kegelschnitt einer Parabel?
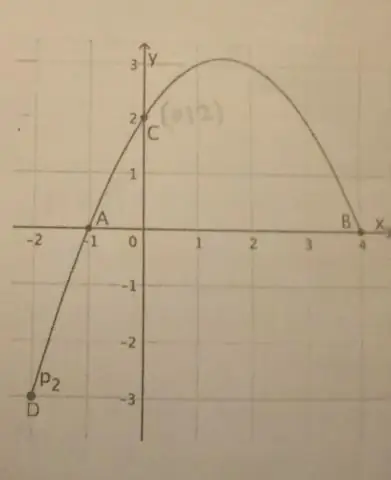
Wenn eine Parabel eine vertikale Achse hat, ist die Standardform der Parabelgleichung diese: (x - h)2 = 4p(y - k), wobei p≠ 0. Der Scheitelpunkt dieser Parabel liegt bei (h, k). Der Fokus liegt bei (h, k + p). Die Leitlinie ist die Gerade y = k - p