Video: Wie findet man die Komponentenform eines Vektors bei gegebenem Betrag und Winkel?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
VIDEO
Ist 0 in Anbetracht dessen ein Einheitsvektor?
EIN Einheitsvektor ist ein Vektor die eine Größe von 1 hat. Die Notation repräsentiert die Norm oder Größe von Vektor v. Das Grundlegende Einheitsvektoren bin ich = (1, 0 ) und j = ( 0 , 1), die die Länge 1 haben und Richtungen entlang der positiven x-Achse bzw. y-Achse haben.
Außerdem, wie sieht die Komponentenform aus? Die Komponentenform eines Vektors ist das geordnete Paar, das die Änderungen der x- und y-Werte beschreibt. In der Grafik oben x1=0, y1=0 und x2=2, ja2=5. Zwei Vektoren sind gleich, wenn sie den gleichen Betrag und die gleiche Richtung haben. Sie sind parallel, wenn sie die gleiche oder entgegengesetzte Richtung haben.
Außerdem, was meinst du mit Größe?
In der Physik, Größe bedeutet Größe oder Ausdehnung. Ein Vektor hat a Größe und eine Richtung, seine Größe ist der numerische Wert seiner Länge, Größe oder Menge. Ein Skalar in der Physik ist definiert durch Größe oder Menge und nicht nach Richtung.
Wie findet man Betrag und Winkel eines Vektors?
- Wende die Gleichung an. um die Größe zu finden, die 1,4 beträgt.
- Wende die Gleichung Theta = tan. an–1(y/x), um den Winkel zu finden: tan–1(1,0/–1,0) = –45 Grad. Beachten Sie jedoch, dass der Winkel tatsächlich zwischen 90 Grad und 180 Grad liegen muss, da die erste Vektorkomponente negativ und die zweite positiv ist.
Empfohlen:
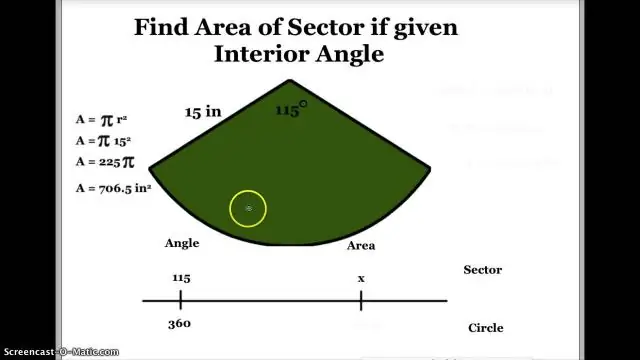
Wie findet man den Zentriwinkel bei gegebener Fläche und Radius eines Sektors?
Bestimmung des Zentralwinkels aus der Sektorfläche (πr2) × (Zentralwinkel in Grad ÷ 360 Grad) = Sektorfläche. Wird der Zentriwinkel im Bogenmaß gemessen, lautet die Formel stattdessen: Sektorfläche = r2 × (Zentralwinkel im Bogenmaß ÷ 2). (θ ÷ 360 Grad) × πr2. (52,3 100π) × 360. (52,3 ÷ 314) × 360
Wie finden Sie die Länge bei gegebenem Volumen?
Maßeinheiten Volumen = Länge x Breite x Höhe. Sie müssen nur eine Seite kennen, um das Volumen eines Würfels zu berechnen. Die Maßeinheiten für das Volumen sind kubische Einheiten. Volumen ist dreidimensional. Sie können die Seiten in beliebiger Reihenfolge multiplizieren. Welche Seite Sie Länge, Breite oder Höhe nennen, spielt keine Rolle
Wie findet man die Komponentenform von zwei Punkten?
Gegeben sind zwei Punktvektoren, von denen einer den Anfangspunkt und der andere den Endpunkt darstellt. Die Komponentenform des durch die beiden Punktvektoren gebildeten Vektors ergibt sich aus den Komponenten des Endpunktes minus den entsprechenden Komponenten des Anfangspunktes
Wie findet man die Länge eines Rechtecks bei gegebenem Umfang?
Ermitteln von Länge und Breite, wenn Sie Fläche und Umfang kennen Wenn Sie die Entfernung um das Rechteck herum kennen, also seinen Umfang, können Sie ein Gleichungspaar für L und W lösen. Die erste Gleichung ist die für Fläche, A = L ⋅ W, und die zweite ist die für den Umfang, P = 2L + 2W
Wie findet man den Winkel eines Sektors in einem Kreisdiagramm?
1 Antwort In jedem Sektor sind 3 Teile zu berücksichtigen: Die Bogenlänge ist ein Bruchteil des Umfangs. Die Sektorfläche ist ein Bruchteil der Gesamtfläche. Der Sektorwinkel ist ein Bruchteil von 360°. Wenn der Sektor 20 % des Kreisdiagramms ausmacht, beträgt jeder dieser Teile 20 % des Ganzen. 20%×360° 20100×360=72°