
Inhaltsverzeichnis:
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:32.
- Zuletzt bearbeitet 2025-01-22 16:55.
Logarithmische Funktionen grafisch darstellen
- Die Graph von invers Funktion von irgendwelchen Funktion ist das Spiegelbild der Graph des Funktion über die Linie y=x.
- Die logarithmische Funktion , y= Protokoll b(x), kann um k Einheiten vertikal und h Einheiten horizontal verschoben werden mit der Gleichung y= Protokoll b(x+h)+k.
- Bedenke die logarithmische Funktion j=[ Protokoll 2(x+1)−3].
Wie stellt man in Anbetracht dessen negative Logs grafisch dar?
Die erste ist, wenn wir a. haben Negativ Unterschrift. Wenn dies passiert, ist unser Graph kippt, entweder über die y-Achse oder über die x-Achse. Die Achse, die die Graph überschlägt, hängt davon ab, wo die Negativ Zeichen ist. Wenn das Negativ Zeichen ist innerhalb des Arguments für die Log-Funktion , das Graph dreht sich um die y-Achse.
Ebenso, was ist ein logarithmisches Funktionsbeispiel? Logarithmus , der Exponent oder die Potenz, auf die eine Basis erhöht werden muss, um eine gegebene Zahl zu erhalten. Mathematisch ausgedrückt ist x der Logarithmus von n zur Basis b wenn bx = n, dann schreibt man x = logB n. Zum Beispiel , 23 = 8; daher ist 3 die Logarithmus von 8 zur Basis 2 oder 3 = log2 8.
Was sind logarithmische Funktionen?
Logarithmische Funktionen sind die Umkehrungen von Exponential Funktionen . Die Umkehrung der Exponentialfunktion Funktion y = ax ist x = aja. Die logarithmische Funktion y = logeinx ist äquivalent zur Exponentialgleichung x = aja. y = logeinx nur unter folgenden Bedingungen: x = aja, a > 0 und a≠1.
Warum verwenden wir logarithmische Graphen?
Dort sind zwei Hauptgründe dafür logarithmisch verwenden Skalen in Diagrammen und Grafiken . Der erste ist auf Schiefe gegenüber großen Werten reagieren; d.h. Fälle, in denen ein oder wenige Punkte sind viel größer als der Großteil der Daten. Der Zweite ist um die prozentuale Änderung oder multiplikative Faktoren anzuzeigen.
Empfohlen:
Wie zeichnet man eine hyperbolische Funktion?

Graphen hyperbolischer Funktionen sinh(x) = (e x - e -x)/2. cosh(x) = (e x + e –x)/2. tanh(x) = sinh(x) / cosh(x) = (ex - e -x) / (ex + e -x) coth(x) = cosh(x) / sinh(x) = (ex + e - x) / (ex - e -x) sech(x) = 1 / cosh(x) = 2 / (ex + e -x) csch(x) = 1 / sinh(x) = 2 / (ex - e - x)
Wie zeichnet man ein Freikörperdiagramm?

Um ein Freikörperdiagramm zu zeichnen, zeichnen wir das interessierende Objekt, zeichnen alle auf dieses Objekt wirkenden Kräfte und lösen alle Kraftvektoren in x– und y-Komponenten auf. Wir müssen für jedes Objekt im Problem ein separates Freikörperdiagramm zeichnen
Wie zeichnet man eine Pflanzenzelle?

VIDEO Wie zeichnet man dann Schritt für Schritt eine Pflanze? Schritte Sammeln Sie, was Sie brauchen. Beginnen Sie die Grundstruktur mit einem Rechteck, aus dem eine Linie herausragt. Machen Sie einen Tisch unter dem Rechteck (das später zum Topf wird).
Wie zeichnet man Biologie?
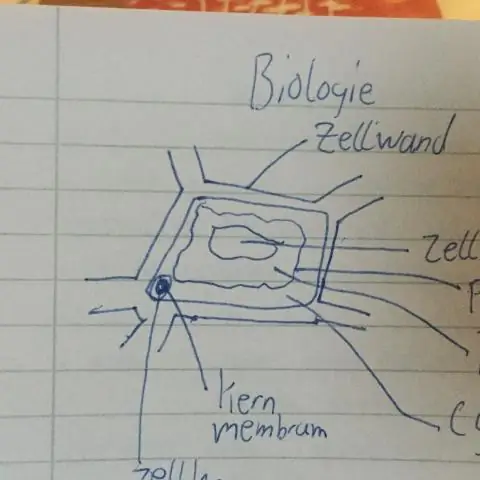
So erstellen Sie ein Diagramm Identifizieren Sie Ihre unabhängigen und abhängigen Variablen. Wählen Sie den richtigen Graphentyp, indem Sie bestimmen, ob jede Variable stetig ist oder nicht. Bestimmen Sie die Werte, die auf die X- und Y-Achse gehen. Beschriften Sie die X- und Y-Achse, einschließlich der Einheiten. Stellen Sie Ihre Daten grafisch dar
Wie zeichnet man logarithmische Funktionen auf einem Taschenrechner?

Auf dem Grafikrechner ist der Logarithmus zur Basis e die ln-Taste. Alle drei sind gleich. Wenn Sie über die logBASE-Funktion verfügen, kann diese verwendet werden, um die Funktion einzugeben (siehe Y1 unten). Wenn nicht, verwenden Sie die Formel für die Änderung der Basis (siehe in Y2 unten)
