Inhaltsverzeichnis:
Video: Wie zeichnet man eine hyperbolische Funktion?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:33
Graphen hyperbolischer Funktionen
- sinh(x) = (e x - e -x)/2.
- cosh(x) = (e x + e -x)/2.
- tanh(x) = sinh(x) / cosh(x) = (e x - e -x) / (e x + e -x)
- coth(x) = cosh(x) / sinh(x) = (e x + e -x) / (e x - e -x)
- sech(x) = 1 / cosh(x) = 2 / (e x + e -x)
- csch(x) = 1 / sinh(x) = 2 / (e x - e -x)
Was ist dann eine Cosh-Funktion?
Y = cosh(X) liefert die hyperbolische Kosinus der Elemente von X. Die cosh-Funktion arbeitet elementweise auf Arrays. Die Funktion akzeptiert sowohl reelle als auch komplexe Eingaben. Alle Winkel sind im Bogenmaß angegeben.
Was ist ein hyperbolisches Beispiel? hyper·bol·isch. Verwenden hyperbolisch in einem Satz. Adjektiv. Die Definition von hyperbolisch ist etwas, das übertrieben oder über das Vernünftige hinaus erweitert wurde. Ein Beispiel von etwas, das beschrieben werden würde als hyperbolisch ist eine Reaktion einer Person, die in keinem Verhältnis zu den eintretenden Ereignissen steht.
Was ist in diesem Zusammenhang Sinh und Cosh?
Die beiden grundlegenden hyperbolischen Funktionen sind: sinh und cosh . (ausgesprochen "shine" und " cosh ") sinh x = ex − e−x 2. cosh x = ex + e−x 2.
Was ist der Sinn der hyperbolischen Funktionen?
Hyperbolische Funktionen erfüllen auch Identitäten analog denen der gewöhnlichen trigonometrischen Funktionen und haben wichtige physikalische Anwendungen. Zum Beispiel die hyperbolisch Kosinus Funktion kann verwendet werden, um den Kurvenverlauf einer zwischen zwei Türmen hängenden Hochspannungsleitung zu beschreiben (siehe Oberleitung).
Empfohlen:
Wie stellt man fest, ob eine Funktion eine horizontale Tangente hat?
Horizontale Linien haben eine Steigung von Null. Wenn die Ableitung null ist, ist die Tangente daher horizontal. Um horizontale Tangenten zu finden, verwenden Sie die Ableitung der Funktion, um die Nullstellen zu lokalisieren und sie wieder in die ursprüngliche Gleichung einzufügen
Wie zeichnet man eine Pflanzenzelle?
VIDEO Wie zeichnet man dann Schritt für Schritt eine Pflanze? Schritte Sammeln Sie, was Sie brauchen. Beginnen Sie die Grundstruktur mit einem Rechteck, aus dem eine Linie herausragt. Machen Sie einen Tisch unter dem Rechteck (das später zum Topf wird).
Wie erkennt man, ob eine Funktion keine Funktion ist?
Die Bestimmung, ob eine Relation eine Funktion in einem Graphen ist, ist mit Hilfe des vertikalen Linientests relativ einfach. Wenn eine senkrechte Linie die Relation im Graphen nur einmal an allen Stellen schneidet, ist die Relation eine Funktion. Wenn jedoch eine vertikale Linie die Relation mehr als einmal schneidet, ist die Relation keine Funktion
Wie zeichnet man in Civil 3d eine Kurve?
So erstellen Sie Kurven vom Ende eines Objekts Klicken Sie auf Registerkarte Start Gruppe Zeichnen Dropdown-Liste Kurven Erstellen Kurve vom Ende des Objekts Suchen. Wählen Sie die Linie oder den Bogen aus, die dem Ende am nächsten liegen, an dem der neue Tangentenbogen angebracht werden soll. Geben Sie einen der folgenden Eingabetypen an: Punkt: Geben Sie P ein und geben Sie dann das Ende des Akkords an. Führen Sie einen der folgenden Schritte aus:
Wie zeichnet man eine Gleichung Schritt für Schritt?
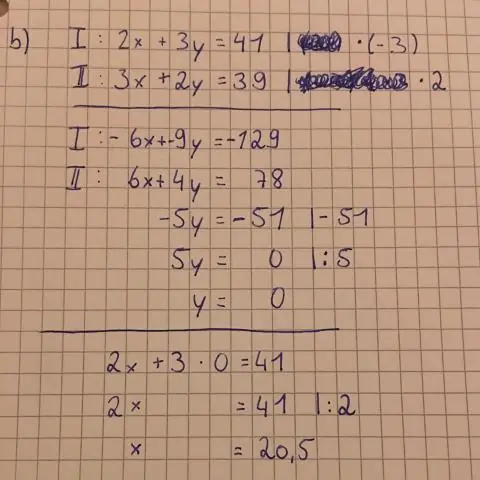
Hier sind einige Schritte: Setze x = 0 in die Gleichung ein und löse nach y auf. Zeichnen Sie den Punkt (0, y) auf der y-Achse. Setze y = 0 in die Gleichung ein und löse nach x auf. Plotten Sie den Punkt (x,0) auf der x-Achse. Zeichne eine gerade Linie zwischen den beiden Punkten