
Inhaltsverzeichnis:
- Autor Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:32.
- Zuletzt bearbeitet 2025-01-22 16:55.
Die Beschränkung ist, dass der Nenner nicht gleich Null sein kann. Da in diesem Problem 4x im Nenner ist, kann es nicht gleich Null sein. Um die zu finden Einschränkungen auf einen rational finden Sie die Werte der Variablen, die den Nenner gleich 0 machen.
Kann ein rationaler Ausdruck auf diese Weise keine Einschränkungen haben?
Na das gleiche ist wahr für rationale Ausdrücke . Der Zweite rationaler Ausdruck ist niemals Null im Nenner und so tun wir es nicht brauchen sich Sorgen machen um irgendwelche Einschränkungen . Beachten Sie auch, dass der Zähler der Sekunde rationaler Ausdruck wird Null sein. Dass ist Okay, wir haben nur brauchen um eine Division durch Null zu vermeiden.
Und warum geben wir Einschränkungen für rationale Ausdrücke an und wann geben wir die Einschränkungen an? Antwort vom Experten bestätigt Rationale Ausdrücke sind solche, die Bruchterme haben. Wir nennen Einschränkungen da dies dazu führen kann, dass die Gleichung in einigen Werten von x undefiniert ist. Das Üblichste Einschränkung für rationale Ausdrücke ist N/0. Das bedeutet, dass jede durch Null geteilte Zahl undefiniert ist.
Wenn man dies berücksichtigt, was sind Einschränkungen in der Algebra?
Die Werte, die den Nenner für einen rationalen Ausdruck gleich Null machen, heißen eingeschränkt Werte. Wir finden diese Werte, indem wir unseren Nenner gleich Null setzen und die resultierende Gleichung lösen.
Wie löst man rationale Ausdrücke?
Die Schritte zum Lösen einer rationalen Gleichung sind:
- Finden Sie den gemeinsamen Nenner.
- Alles mit dem gemeinsamen Nenner multiplizieren.
- Vereinfachen.
- Überprüfen Sie die Antwort(en), um sicherzustellen, dass es keine überflüssige Lösung gibt.
Empfohlen:
Was ist der Unterschied zwischen einem ultramafischen, einem mafischen, einem intermediären und einem felsischen Gestein?

In einem allgemein anerkannten Klassifikationsschema für den Kieselsäuregehalt werden Gesteine mit mehr als 65 Prozent Kieselsäure als felsisch bezeichnet; diejenigen mit zwischen 55 und 65 Prozent Siliziumdioxid sind Zwischenprodukte; diejenigen mit zwischen 45 und 55 Prozent Siliziumdioxid sind mafisch; und diejenigen mit weniger als 45 Prozent sind ultramafisch
Was ist ein Ausdruck, der eine oder mehrere Variablen enthält?
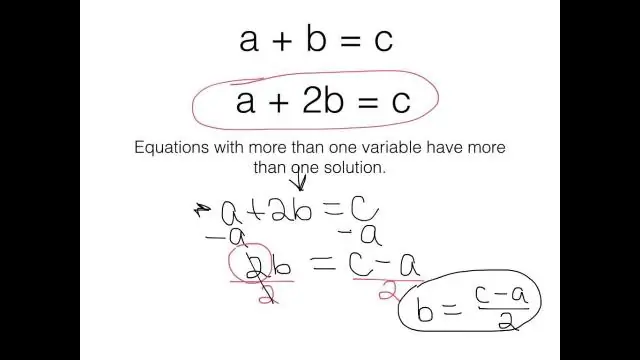
Ein algebraischer Ausdruck ist ein Ausdruck, der eine oder mehrere Variablen enthält. Eine algebraische Gleichung ist eine Gleichung, die eine oder mehrere Variablen enthält
Warum geben wir Einschränkungen für den rationalen Ausdruck an und wann geben wir die Einschränkungen an?

Wir geben Einschränkungen an, da dies dazu führen kann, dass die Gleichung in einigen Werten von x undefiniert ist. Die häufigste Einschränkung für rationale Ausdrücke ist N/0. Das bedeutet, dass jede durch Null geteilte Zahl undefiniert ist. Zum Beispiel für die Funktion f(x) = 6/x², wenn Sie x=0 ersetzen, würde dies zu 6/0 führen, was undefiniert ist
Was ist ein Ausdruck, der Variablen Zahlen und mindestens eine Operation kombiniert?

Ein numerischer Ausdruck enthält Zahlen und Operationen. Ein algebraischer Ausdruck ist fast genau derselbe, außer dass er auch Variablen enthält
Was ist der Unterschied zwischen einem Verhältnis, einem Anteil und einem Satz?

Ein Verhältnis vergleicht die Größe zweier Größen. Wenn die Mengen unterschiedliche Einheiten haben, wird ein Verhältnis als Rate bezeichnet. Ein Anteil ist eine Aussage über die Gleichheit zweier Verhältnisse
