Video: Was ist die asymptotische Notation, um die große 0-Notation zu erklären?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
Big-O . Big-O , allgemein geschrieben als Ö , ist ein Asymptotische Notation für den schlimmsten Fall oder die Wachstumsgrenze für eine gegebene Funktion. Es bietet uns eine asymptotisch obere Schranke für die Wachstumsrate der Laufzeit eines Algorithmus.
Ebenso fragen die Leute, was Sie mit Big-O-Notation meinen?
Große O-Notation wird in der Informatik verwendet, um die Leistung oder Komplexität eines Algorithmus zu beschreiben. Großes O beschreibt speziell das Worst-Case-Szenario und kann verwendet werden, um die benötigte Ausführungszeit oder den belegten Platz (z. B. im Arbeitsspeicher oder auf der Festplatte) durch einen Algorithmus zu beschreiben.
Warum ist die Big-O-Notation wichtig? Große O-Notation ermöglicht die Analyse von Algorithmen im Hinblick auf Gesamteffizienz und Skalierbarkeit. Es abstrahiert konstante Ordnungsunterschiede in der Effizienz, die von Plattform, Sprache, Betriebssystem variieren können, um sich auf die inhärente Effizienz des Algorithmus zu konzentrieren und wie er sich je nach Größe der Eingabe ändert.
Ist die Big-O-Notation dann der Worst-Case?
Obwohl große o-Notation hat nichts damit zu tun schlimmsten Fall Analyse vertreten wir in der Regel die schlimmsten Fall von große o-Notation . Also, bei der binären Suche das Beste Fall ist Ö (1), Durchschnitt und schlimmsten Fall ist Ö (einloggen). Kurz gesagt, es gibt keine Art von Beziehung vom Typ „ großes O wird verwendet für schlimmsten Fall , Theta für Durchschnitt Fall ”.
Was ist Big O und Small O Notation?
Groß - Ö ist eine inklusive Obergrenze, während wenig - Ö ist eine strenge Obergrenze. Die Funktion f(n) = 3n lautet beispielsweise: in Ö (n²), Ö (n²) und Ö (n)
Empfohlen:
Was ist verbundener Graph mit Beispiel erklären?
In einem vollständigen Graphen gibt es zwischen jedem einzelnen Knotenpaar im Graphen eine Kante. Das zweite ist ein Beispiel für einen zusammenhängenden Graphen. In einem verbundenen Graphen ist es möglich, von jeder Ecke des Graphen zu jeder anderen Ecke des Graphen durch eine Reihe von Kanten zu gelangen, die als Pfad bezeichnet werden
Wie ist die Translation von mRNA terminiert zu erklären?
Die Translation von mRNA wird beendet, wenn ein Stopcodon (UAA, UAG, UGA) die A-Stelle des Ribosoms besetzt. Stoppcodons werden von tRNAs nicht erkannt und daher bindet ein Release Factor (RF)-Protein an den Komplex und hydrolysiert die Bindung zwischen letzter tRNA und Aminosäure
Was ist Phoresis mit Beispiel erklären?
Phorese. Sowohl Kommensalismus als auch Phorese können eher als räumliche als als physiologische Beziehungen angesehen werden. Beispiele für Phorese sind die zahlreichen sesshaften Protozoen, Algen und Pilze, die sich an den Körpern von Wasserarthropoden, Schildkröten usw
Wie können Wasserstoffbrückenbindungen zwischen Wassermolekülen dazu beitragen, die Fähigkeit von Wasser zu erklären, große Energiemengen vor der Verdampfung zu absorbieren?
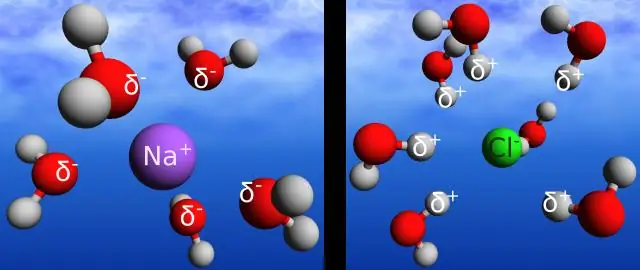
Durch die Wasserstoffbrückenbindungen im Wasser kann es Wärmeenergie langsamer aufnehmen und abgeben als viele andere Stoffe. Die Temperatur ist ein Maß für die Bewegung (kinetische Energie) von Molekülen. Wenn die Bewegung zunimmt, ist die Energie höher und damit die Temperatur höher
Was ist die Drake-Gleichung vollständig zu erklären?
Die Drake-Gleichung ist ein probabilistisches Argument, das verwendet wird, um die Anzahl aktiver, kommunikativer außerirdischer Zivilisationen in der Milchstraße abzuschätzen