
Inhaltsverzeichnis:
- Autor Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:32.
- Zuletzt bearbeitet 2025-06-01 05:03.
Zu algebra machen , lösen Sie Probleme immer in der Reihenfolge der Operationen, die aus Klammern, Exponenten, Multiplikation, Division, Addition und Subtraktion besteht. Zum Beispiel würdest du zuerst alles lösen, was in Klammern steht, dann die Exponenten und dann tun jede Multiplikation und so weiter.
Wissen Sie auch, was sind die Grundregeln der Algebra?
Die Basic Gesetze von Algebra sind die assoziativen, kommutativen und distributiven Gesetze. Sie helfen, den Zusammenhang zwischen Zahlenoperationen zu erklären und helfen, Gleichungen zu vereinfachen oder zu lösen. Die Anordnung der Addends hat keinen Einfluss auf die Summe. Die Anordnung der Faktoren hat keinen Einfluss auf das Produkt.
Abgesehen davon, wie geht man vor der Algebra? Konzentrieren Sie sich darauf, die Grundlagen gut zu lernen, und Sie werden in der Lage sein, eine anspruchsvolle Pre-Algebra-Klasse mit Leichtigkeit zu bestehen.
- Terminologie der Präalgebra. Das Auswendiglernen von Vokabeln scheint nicht viel Spaß zu machen, aber die Präalgebra basiert auf der grundlegenden Terminologie.
- Gleichungen verstehen.
- Verfolgen Sie Ihre Arbeit.
- Hilfe erhalten.
Ebenso fragen die Leute, wofür verwendet man Algebra?
Manche Schüler denken, dass Algebra ist wie das Erlernen einer anderen Sprache. Dies trifft in geringem Maße zu, Algebra ist eine einfache Sprache, die verwendet wird, um Probleme zu lösen, die nicht allein durch Zahlen gelöst werden können. Es modelliert reale Situationen, indem es Symbole wie die Buchstaben x, y und z verwendet, um Zahlen darzustellen.
Wie lauten die Formeln der Algebra?
Algebra Formeln
- (a + b) 2 = a 2 + b 2 + 2ab.
- (a - b) 2 = a 2 + b 2 − 2ab.
- ein 2 − b 2 = (a − b) (a + b)
- (x + a) (x + b) = x 2 + (a + b) x + ab.
- (a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2bc + 2ca.
- (a + (−b) + (−c)) 2 = a 2 + (−b) 2 + (−c) 2 + 2a (−b) + 2 (−b) (−c) + 2a (−c) (a - b - c) 2 = a 2 + b 2 + c 2 − 2ab + 2bc − 2ca.
Empfohlen:
Wie macht man Salzschneeflocken mit Kristallen?

Anleitung: Kochen Sie Wasser und gießen Sie es in eine Tasse, die heißes Wasser aushält. Fügen Sie ein paar Teelöffel Salz hinzu und rühren Sie mit dem Pinsel, bis es sich löst. Geben Sie immer teelöffelweise Salz hinzu, bis es sich nicht mehr auflöst und sich auch nach längerem Rühren Salzkristalle am Boden der Tasse befinden
Wie macht man Diamanten aus Graphit?

Eine Möglichkeit, Graphit in Diamant zu verwandeln, besteht darin, Druck auszuüben. Da Graphit jedoch unter normalen Bedingungen die stabilste Form von Kohlenstoff ist, ist dafür etwa das 150.000-fache des atmosphärischen Drucks an der Erdoberfläche erforderlich. Jetzt ist ein alternativer Weg, der auf der Nanoskala funktioniert, in Reichweite
Wie wenden Sie das grundlegende Zählprinzip an?

Das grundlegende Zählprinzip (auch Zählregel genannt) ist eine Möglichkeit, die Anzahl der Ergebnisse in einem Wahrscheinlichkeitsproblem zu ermitteln. Grundsätzlich multiplizieren Sie die Ereignisse miteinander, um die Gesamtzahl der Ergebnisse zu erhalten
Was bedeutet Macht zu einer Macht?

Definition. Ein anderes Wort, das verwendet wird, um einen Exponenten zu beschreiben, ist Macht. Wenn Sie also den Ausdruck potenzieren hören, bedeutet dies nur, einen Exponenten zu einem anderen zu erheben. Egal in welcher Form der Exponent auftritt, die gleiche Regel gilt für die Berechnung einer Potenz in eine Potenz. Die Regel ist, die Exponenten miteinander zu multiplizieren
Wie befähigen Zellstrukturen eine Zelle, grundlegende Lebensprozesse durchzuführen?
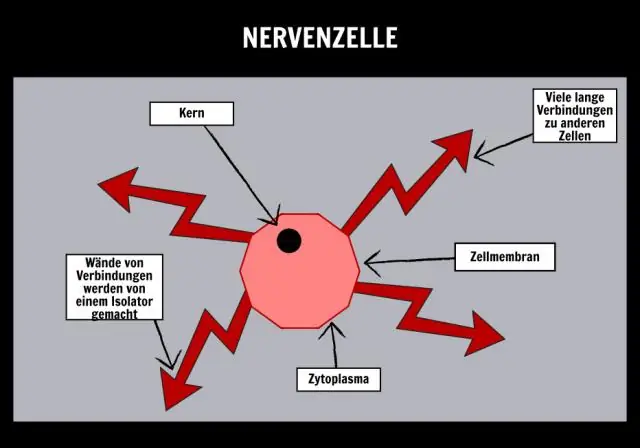
Spezialisierte Zellen erfüllen besondere Funktionen wie Photosynthese und Energieumwandlung. Zytoplasma, das von einer Zellmembran umgeben ist und die grundlegenden Lebensprozesse ausführt. und Organelle in einer Zelle führen bestimmte Prozesse durch, wie zum Beispiel die Herstellung oder Speicherung von Substanzen, die der Zelle helfen, am Leben zu bleiben
