
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:32.
- Zuletzt bearbeitet 2025-01-22 16:55.
Die Chi-Quadrat-Verteilung ist die Verteilung der Summe der quadrierten Standardnormalabweichungen. Die Freiheitsgrade der Verteilung gleich der Anzahl der aufsummierten Standard-Normalabweichungen ist. Die Mittelwert einer Chi-Quadrat-Verteilung sind seine Freiheitsgrade.
Was ist die Chi-Quadrat-Verteilung mit Beispielen?
Die Chi - Quadratische Verteilung Die Chi-Quadrat-Verteilung ist der Verteilung der Summe dieser zufälligen Proben quadriert . Die Freiheitsgrade (k) sind gleich der Anzahl der Proben summiert wird. Zum Beispiel , wenn Sie 10. genommen haben Proben von der normalen Verteilung , dann df = 10.
Benötigt das Chi-Quadrat eine Normalverteilung? 2 Antworten. Normalität ist Voraussetzung für die Chi-Quadrat Testen Sie, dass eine Varianz einem bestimmten Wert entspricht, aber es gibt viele Tests, die aufgerufen werden chi - Quadrat weil ihre asymptotische null Verteilung ist chi - Quadrat so wie die chi - Quadrat Unabhängigkeitstest in Kontingenztafeln und Chi-Quadrat Eignungstest.
Man kann sich auch fragen, warum die Chi-Quadrat-Verteilung immer positiv ist?
Der berechnete Wert von Chi - Quadrat ist immer positiv denn der Unterschied zwischen der beobachteten Frequenz und der erwarteten Frequenz ist kariert , das heißt (O - E)2 und der Demoninator ist die erwartete Zahl, die auch sein muss positiv . Die Chi - Quadratische Verteilung ist positiv verzerrt.
Was sind Chi-Quadrat-Freiheitsgrade?
Die Freiheitsgrade für die chi - Quadrat werden wie folgt berechnet Formel : df = (r-1)(c-1) wobei r die Anzahl der Zeilen und c die Anzahl der Spalten ist. Wenn das Beobachtete chi - Quadrat Teststatistik größer als der kritische Wert ist, kann die Nullhypothese verworfen werden.
Empfohlen:
Was ist der Unterschied zwischen Mittelwert und Varianz?

Was ist der Unterschied zwischen Mittelwert und Varianz? Einfach ausgedrückt: Der Mittelwert ist das arithmetische Mittel aller Zahlen, das arithmetische Mittel. Die Varianz ist eine Zahl, die uns eine Vorstellung davon gibt, wie seltsam diese Zahlen sein könnten, mit anderen Worten, ein Maß dafür, wie stark sie variieren
Wie finden Sie die fehlende Zahl, wenn der Mittelwert angegeben wird?

Der Mittelwert einer Reihe von Zahlen ist der Durchschnitt dieser Zahlen. Sie können den Mittelwert ermitteln, indem Sie den Zahlensatz addieren und durch die Anzahl der angegebenen Zahlen dividieren. Wenn Sie den Mittelwert erhalten und aufgefordert werden, eine fehlende Zahl aus dem Satz zu finden, verwenden Sie eine einfache Gleichung
Wie finden Sie Standardabweichung und Mittelwert in Excel?
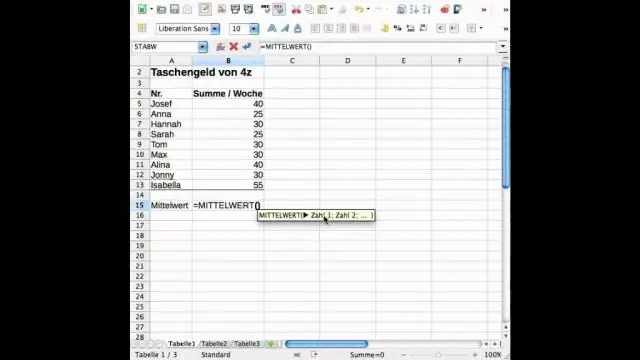
Die Standardabweichung ist ein Maß dafür, wie viel Varianz in einer Reihe von Zahlen im Vergleich zum Durchschnitt (Mittelwert) der Zahlen vorhanden ist. Um die Standardabweichung in Excel zu berechnen, können Sie je nach Datensatz eine von zwei Primärfunktionen verwenden. Wenn die Daten die gesamte Bevölkerung repräsentieren, können Sie das STDEV verwenden. Pfunktion
Was ist das Beispiel für den Mittelwert?

Mittelwert: Die 'durchschnittliche' Zahl; gefunden, indem alle Datenpunkte addiert und durch die Anzahl der Datenpunkte geteilt werden.Beispiel: Der Mittelwert von 4, 1 und 7 ist (4 + 1 + 7) / 3= 12 / 3 = 4 (4+1+7)/3 = 12/3 = 4 (4+1+7)/3=12/3=4linke Klammer,4, plus, 1, plus, 7, rechte Klammer, Schrägstrich, 3, gleich, 12,Schräg, 3, gleich, 4
Was ist der Mittelwert der Höhe?

Definition von Höhe. 1: die Höhe, auf die etwas angehoben wird: wie. a: der Winkelabstand von etwas (z. B. einem Himmelsobjekt) über dem Horizont. b: der Grad, in dem eine Waffe über den Horizont gerichtet ist. c: die Höhe über dem Meeresspiegel: Höhe
