Video: Was ist die Vorwärtsphase des Zeilenreduktionsprozesses?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
Die Drehpositionen in a Matrix werden vollständig durch die Positionen der führenden Einträge in den Reihen ungleich null jeder Staffelform bestimmt, die aus dem Matrix . Reduzieren von a Matrix in Staffelform wird die Vorwärtsphase des Zeilenreduktionsprozesses genannt.
Was ist dementsprechend der Zeilenreduktionsalgorithmus?
Gaußsche Elimination, auch bekannt als Reihenreduzierung , ist ein Algorithmus in der linearen Algebra zum Lösen eines linearen Gleichungssystems. Es wird normalerweise als eine Folge von Operationen verstanden, die an der entsprechenden Koeffizientenmatrix ausgeführt werden. Die Methode ist nach Carl Friedrich Gauß (1777–1855) benannt.
Was sind außerdem elementare Zeilenoperationen von Matrizen? Elementare Operationen Multiplizieren Sie jedes Element in a Reihe (oder Spalte) durch eine Zahl ungleich Null. Multiplizieren Sie a Reihe (oder Spalte) durch eine Zahl ungleich Null und addiere das Ergebnis zu einer anderen Reihe (oder Spalte).
Wissen Sie auch, ob der Zeilenreduktionsalgorithmus nur für erweiterte Matrizen gilt?
Die Der Zeilenreduktionsalgorithmus gilt nur für erweiterte Matrizen für ein lineares System. Antwort: Falsch. Irgendein Matrix kann Sein reduziert . Wenn man Reihe in einer Staffelform von an erweiterte Matrix [0 0 0 5 0] ist, dann ist das zugehörige lineare System inkonsistent.
Können Sie Row reduzieren, bevor Sie eine Determinante finden?
Bestimmend einer oberen (unteren) Dreiecks- oder Diagonalmatrix gleich dem Produkt ihrer diagonalen Einträge. detA =detAT, also wir kann entweder bewerben Reihe oder Spaltenoperationen, um die bestimmend . 2. Wenn zwei Reihen oder zwei Spalten von A sind identisch oder wenn A hat a Reihe oder eine Spalte mit Nullen, dann ist detA = 0.
Empfohlen:
Was war die erste Theorie, die 1644 von Rene Descartes zur Erklärung des Ursprungs des Sonnensystems vorgeschlagen wurde?
Die am weitesten verbreitete Theorie der Planetenentstehung, bekannt als die Nebelhypothese, behauptet, dass das Sonnensystem vor 4,6 Milliarden Jahren durch den Gravitationskollaps einer riesigen Molekülwolke mit einem Durchmesser von Lichtjahren entstanden ist
Warum ist die EMF Null, wenn die Spule genau durch die Mitte des Magneten läuft?
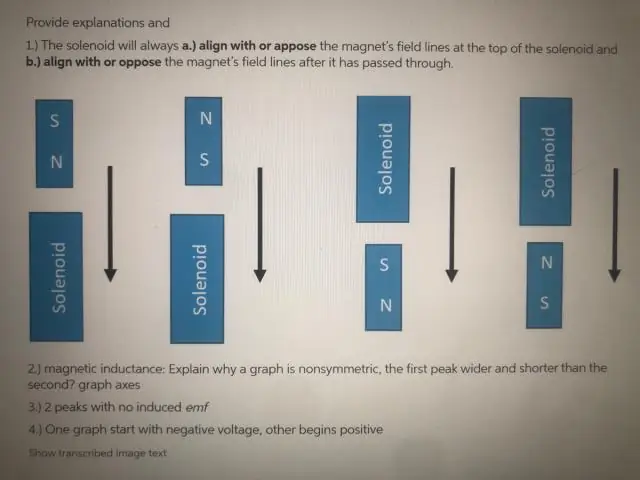
Die EMK ist nur für einen Moment Null, wenn der Magnet genau durch die Mitte der Spule geht. Dies liegt daran, dass die Wirkung des N-Pols am einen Ende des Magneten an diesem Ende der Spule durch die Wirkung des S-Pols des Magneten am anderen Ende der Spule genau aufgehoben wird
Wie wirkt sich die Änderung der Masse des Skaters auf die potentielle Energie des Skaters aus?
Masse beeinflusst/beeinflusst nicht die Energiemenge. Ein sich immer schneller bewegendes Objekt hat eine kinetische Energie, die zunimmt / abnimmt / gleich bleibt. Ein Objekt, das sich immer schneller bewegt, hat eine potenzielle Energie, die zunimmt / abnimmt / gleich bleibt
Wie würde sich die Ausbreitung des Meeresbodens auf die Größe des Meeresbodens auswirken?
Mittelozeanische Rücken und die Ausbreitung des Meeresbodens können ebenfalls den Meeresspiegel beeinflussen. Wenn sich die ozeanische Kruste von den flachen mittelozeanischen Rücken entfernt, kühlt sie ab und sinkt, wenn sie dichter wird. Dies erhöht das Volumen des Meeresbeckens und senkt den Meeresspiegel
Ist der Himmel wegen des Ozeans blau oder ist der Ozean wegen des Himmels blau?
„Der Ozean sieht blau aus, weil Rot, Orange und Gelb (langwelliges Licht) stärker von Wasser absorbiert werden als Blau (kurzwelliges Licht). Wenn also weißes Licht von der Sonne in den Ozean eintritt, ist es meistens das Blau, das zurückgegeben wird. Aus demselben Grund ist der Himmel blau.'