Video: Was ist die hessische Matrixoptimierung?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:33
Verwenden Sie in Optimierung
Hessische Matrizen werden großflächig eingesetzt Optimierung Probleme bei Newton-Methoden, weil sie der Koeffizient des quadratischen Termes einer lokalen Taylorentwicklung einer Funktion sind
Also, wofür wird eine Jacobi-Matrix verwendet?
?ˈko?bi?n/, /d??-, j?-/) einer vektorwertigen Funktion mehrere Variablen sind die Matrix aller seiner partiellen Ableitungen erster Ordnung.
Was sagt uns außerdem die hessische Matrix? In der Mathematik ist die Hessische Matrix oder Hessisch ist ein Quadrat Matrix von partiellen Ableitungen zweiter Ordnung einer skalarwertigen Funktion oder eines Skalarkörpers. Es beschreibt die lokale Krümmung einer Funktion vieler Variablen.
Was ist außerdem ein Gradientenvektor?
Die Gradient ist ein schickes Wort für Ableitung oder die Änderungsrate einer Funktion. Es ist ein Vektor (eine Bewegungsrichtung) das. Zeigt in Richtung der größten Zunahme einer Funktion (Intuition, warum)
Ist Jacobian immer positiv?
Bereiche sind immer positiv , also ist die Fläche eines kleinen Parallelogramms im xy-Raum immer der absolute Wert der Jacobi mal die Fläche des entsprechenden Rechtecks im UV-Raum. Nehmen wir stattdessen x=−5u, sog'(u)=−5 ist negativ. Nun e−x/5=eu und dx=−5du.
Empfohlen:
Warum ist die EMF Null, wenn die Spule genau durch die Mitte des Magneten läuft?
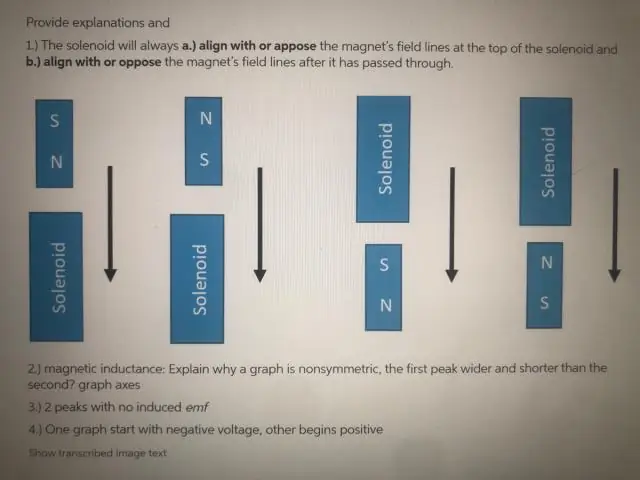
Die EMK ist nur für einen Moment Null, wenn der Magnet genau durch die Mitte der Spule geht. Dies liegt daran, dass die Wirkung des N-Pols am einen Ende des Magneten an diesem Ende der Spule durch die Wirkung des S-Pols des Magneten am anderen Ende der Spule genau aufgehoben wird
Welche Organelle ist für die chemische Energie verantwortlich, die die Zelle zum Funktionieren benötigt?
Funktion der Mitochondrien Mitochondrien werden oft als „Kraftwerke“oder „Energiefabriken“einer Zelle bezeichnet, weil sie für die Herstellung von Adenosintriphosphat (ATP) verantwortlich sind, dem Hauptenergieträger der Zelle
Was passiert während der Interphase in Bezug auf die DNA, die für die Zellteilung wichtig ist?
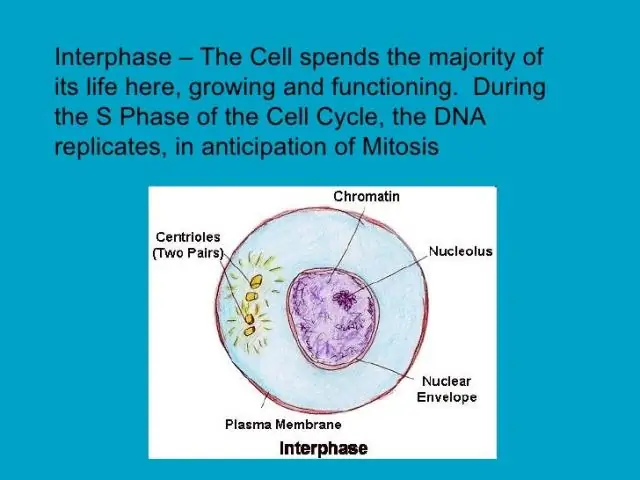
Während der Interphase nimmt eine Zelle an Größe zu, synthetisiert neue Proteine und Organellen, repliziert ihre Chromosomen und bereitet sich auf die Zellteilung vor, indem sie Spindelproteine produziert. Vor der Zellteilung werden Chromosomen repliziert, sodass jedes Chromosom aus zwei identischen „Schwester“-Chromatiden besteht
Ist die Plasmamembran die gleiche wie die Phospholipid-Doppelschicht?
Andere Membranen, die Organellen umgeben, sind ebenfalls Lipiddoppelschichten, und sie verschmelzen oft und klemmen sich von der Plasmamembran ab. Aber sie sind keine Plasmamembran. Während die Plasmamembran also immer (teilweise aus) der Lipiddoppelschicht besteht, ist die Lipiddoppelschicht nicht immer (Teil) der Plasmamembran
Was ist die Substanz, die aus DNA und Proteinen besteht, die eng zusammengepackt sind?
Eukaryotische Chromosomen enthalten sowohl DNA als auch Proteine, die eng zusammengepackt sind, um eine Substanz namens Chromatin zu bilden