Video: Wie findet man Winkelgeschwindigkeit und Beschleunigung?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
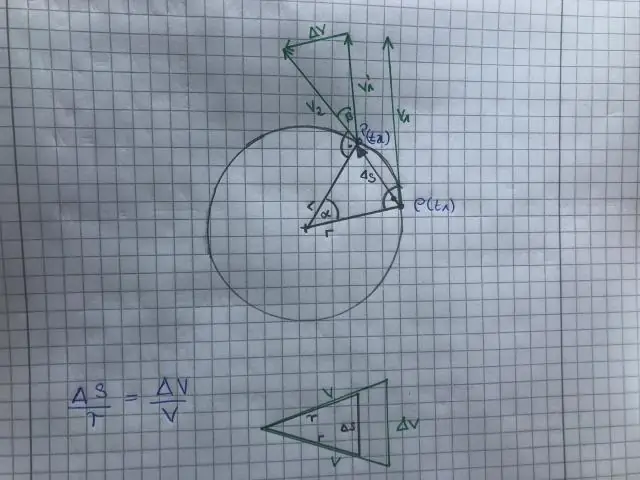
In Gleichungsform, Winkelbeschleunigung wird wie folgt ausgedrückt: α=ΔωΔt α = Δ ω Δ t, wobei Δω die Änderung von ist Winkelgeschwindigkeit und t ist die Zeitänderung. Die Einheiten von Winkelbeschleunigung sind (rad/s)/s oder rad/s2.
Auch gefragt, was ist Winkelgeschwindigkeit und Beschleunigung?
Winkelgeschwindigkeit ist die Rate von Geschwindigkeit bei der sich ein Objekt oder ein Partikel in einem bestimmten Zeitraum um ein Zentrum oder einen bestimmten Punkt dreht. Winkelgeschwindigkeit wird in Winkel pro Zeiteinheit oder Radiant pro Sekunde (rad/s) gemessen. Die Änderungsrate von Winkelgeschwindigkeit ist Winkelbeschleunigung.
Was ist der Unterschied zwischen Winkelgeschwindigkeit und Winkelbeschleunigung? Winkelgeschwindigkeit ist die Anzahl der Drehungen eines Körpers pro Zeiteinheit um seine Drehachse gegen den Uhrzeigersinn Winkelgeschwindigkeit . Winkelbeschleunigung ist die Veränderung in Winkelgeschwindigkeit des Körpers pro Zeiteinheit um seine Rotationsachse, heißt Winkelbeschleunigung.
Man kann sich auch fragen, was ist Winkelbeschleunigung in der Physik?
Winkelbeschleunigung , auch Rotation genannt Beschleunigung , ist ein quantitativer Ausdruck der Änderung in eckig Geschwindigkeit, die ein sich drehendes Objekt pro Zeiteinheit erfährt. Es ist eine Vektorgröße, die aus einer Betragskomponente und einer von zwei definierten Richtungen oder Sinnen besteht.
Was ist die Winkelgeschwindigkeitsformel?
Es ist die Winkeländerung eines sich bewegenden Objekts (gemessen im Bogenmaß), geteilt durch die Zeit. Winkelgeschwindigkeit hat eine Größe (einen Wert) und eine Richtung. Winkelgeschwindigkeit = (Endwinkel) - (Anfangswinkel) / Zeit = Positionsänderung/Zeit. = (θF -ich) / T. = Winkelgeschwindigkeit.
Empfohlen:
Was ist die Einheit der Winkelgeschwindigkeit?
Diese Winkelstrecke, die ein Körper pro Sekunde zurücklegt, wird als „Winkelgeschwindigkeit“bezeichnet. Die SI-Einheit der Winkelgeschwindigkeit ist Radiant pro Sekunde (rad/s)
Wie stellt man Geschwindigkeit und Beschleunigung dar?
Das Prinzip besteht darin, dass die Steigung der Linie in einem Geschwindigkeits-Zeit-Diagramm nützliche Informationen über die Beschleunigung des Objekts liefert. Wenn die Beschleunigung null ist, ist die Steigung null (d. h. eine horizontale Linie). Wenn die Beschleunigung positiv ist, ist die Steigung positiv (d. h. eine nach oben geneigte Linie)
Wie findet man konstante Beschleunigung?
Konstante Beschleunigung Da wir als Basiseinheiten Meter und Sekunden verwenden, messen wir die Beschleunigung in Metern pro Sekunde pro Sekunde. Ändert sich beispielsweise die Geschwindigkeit eines sich geradlinig bewegenden Teilchens gleichmäßig (mit konstanter Änderungsrate) von 2 m/s auf 5 m/s innerhalb einer Sekunde, dann beträgt seine konstante Beschleunigung 3 m/s2
Wie findet man Geschwindigkeit mit Beschleunigung und Zeit?
Wenn die Beschleunigung konstant ist, dann Beschleunigung = Änderung der Geschwindigkeit/Zeit für diese Änderung. Die Geschwindigkeitsänderung ist also die Beschleunigung mal die Zeit. Sie müssen noch die Anfangsgeschwindigkeit kennen, die Sie der Änderung hinzufügen. (Wenn die Beschleunigung nicht konstant ist, benötigen Sie Berechnungen.)
Wie findet man Beschleunigung aus Geschwindigkeit?
Bei der Berechnung der Beschleunigung wird die Geschwindigkeit durch die Zeit dividiert – oder in SI-Einheiten der Meter pro Sekunde [m/s] durch die Sekunde [s]. Die zweimalige Division der Distanz durch die Zeit entspricht der Division der Distanz durch das Quadrat der Zeit. Daher ist die SI-Einheit der Beschleunigung Meter pro Sekunde im Quadrat