
Inhaltsverzeichnis:
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:32.
- Zuletzt bearbeitet 2025-06-01 05:03.
Hat zwei Lösungen x = a und x = -a, weil beide Zahlen im Abstand a von 0 sind. Sie beginnen damit, dass Sie zwei separate Gleichungen bilden und sie dann separat lösen. Ein Absolutwert Gleichung hat keine Lösung, wenn die Absolutwert Ausdruck gleich einer negativen Zahl ist, da an Absolutwert kann nie negativ sein.
Ebenso fragen die Leute, was sind die Regeln für den absoluten Wert?
Wenn wir die nehmen Absolutwert einer Zahl erhalten wir immer eine positive Zahl (oder Null). Unabhängig davon, ob die Eingabe positiv oder negativ (oder null) war, ist die Ausgabe immer positiv (oder null). Zum Beispiel | 3 | = 3 und | -3 | = 3 auch.
Außerdem, woher wissen Sie, ob eine Absolutwertungleichung aus allen reellen Zahlen besteht? Die Absolutwert von irgendeine Nummer ist entweder null (0) oder positiv. Es ergibt Sinn das es muss immer größer sein als irgendein Negativ Nummer . Die Antwort auf diesen Fall ist immer alle reellen Zahlen.
Auch zu wissen, wie man eine Ungleichung graphisch darstellt?
Wie man eine lineare Ungleichung grafisch darstellt
- Ordne die Gleichung so um, dass "y" links und alles andere rechts steht.
- Zeichnen Sie die "y="-Linie (machen Sie eine durchgezogene Linie für y≤ oder y≥ und eine gestrichelte Linie für y)
- Schattierung oberhalb der Linie für "größer als" (y> oder y≥) oder unterhalb der Linie für "kleiner als" (y< oder y≤).
Was ist ein Beispiel für eine zusammengesetzte Ungleichung?
Denken Sie an die Beispiel des zusammengesetzte Ungleichung : x < 5 und x ≧ −1. Die Grafik jedes Einzelnen Ungleichheit wird farbig dargestellt. Da das Wort und die beiden verbindet Ungleichheiten , ist die Lösung die Überlappung der beiden Lösungen. Hier treffen beide Aussagen gleichzeitig zu.
Empfohlen:
Wie schreibt man die Formel für eine Verbindung, die ein mehratomiges Ion enthält?
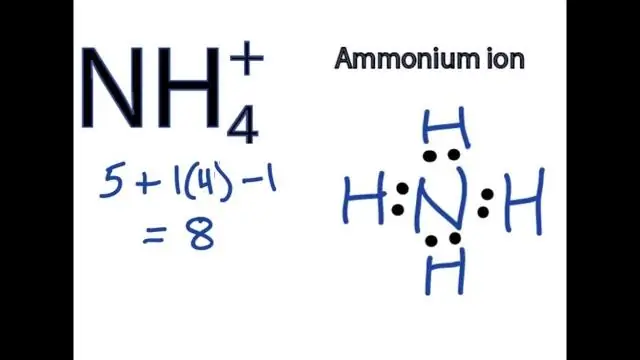
Um Formeln für Verbindungen mit mehratomigen Ionen zu schreiben, schreiben Sie das Symbol für das Metallion gefolgt von der Formel für das mehratomige Ion und gleichen Sie die Ladungen aus. Um eine Verbindung mit einem mehratomigen Ion zu benennen, geben Sie zuerst das Kation und dann das Anion an
Wie schreibt man eine Koordinatenregel für eine Drehung?

Um eine Regel für diese Rotation zu schreiben, würdest du schreiben: R270? (x,y) = (−y,x). Notationsregel Eine Notationsregel hat die Form R180? A → O = R180? (x,y) → (−x,−y) und teilt Ihnen mit, dass das Bild A um den Ursprung gedreht wurde und sowohl die x- als auch die y-Koordinaten mit -1 . multipliziert werden
Wie schreibt man eine Funktionsregel für eine Eingabe-Ausgabe-Tabelle?
Jedes Zahlenpaar in der Tabelle ist durch dieselbe Funktionsregel verbunden. Diese Regel lautet: Multiplizieren Sie jede Eingabenummer (egin{align*}xend{align*}-Wert) mit 3, um die Ausgabenummer (egin{align*}yend{align*}-Wert) zu finden. Sie können eine solche Regel verwenden, um auch andere Werte für diese Funktion zu finden
Wie schreibt man eine Gleichung in Form eines Steigungsabschnitts für eine Tabelle?
Nehmen Sie die Gleichung y = mx + b und setzen Sie den m-Wert (m = 1) und ein Paar von (x, y)-Koordinaten aus der Tabelle ein, z. B. (5, 3). Dann nach b auflösen. Verwenden Sie schließlich die gefundenen m- und b-Werte (m = 1 und b = -2), um die Gleichung zu schreiben
Woher wissen Sie, ob eine Absolutwertungleichung keine Lösung hat?

Okay, wenn absolute Werte immer positiv oder null sind, können sie auf keinen Fall kleiner oder gleich einer negativen Zahl sein. Daher gibt es für beides keine Lösung. Wenn der Absolutwert in diesem Fall positiv oder null ist, ist er immer größer oder gleich einer negativen Zahl
