
Inhaltsverzeichnis:
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:32.
- Zuletzt bearbeitet 2025-01-22 16:55.
Die t Prüfung statistischer Wert zu Prüfung ob die Mittelwerte unterschiedlich sind, kann wie folgt berechnet werden: t=mA−mB√S2nA+S2nB. S2 ist ein Schätzer der gemeinsamen Varianz der beiden Stichproben. Sie lässt sich wie folgt berechnen: S2=∑(x−mA)2+∑(x−mB)2nA+nB−2.
Wie verwendet man einfach die t-Testformel?
T-Test-Formel
- overline{x} = Mittelwert der ersten Wertemenge.
- overline{x}_{2} = Mittelwert des zweiten Wertesatzes.
- S_{1} = Standardabweichung des ersten Wertesatzes.
- S_{2} = Standardabweichung des zweiten Wertesatzes.
- n_{1} = Gesamtzahl der Werte im ersten Satz.
- n_{2} = Gesamtzahl der Werte im zweiten Satz.
Wofür wird der T-Test außerdem verwendet? EIN T - Prüfung ist eine Art von Inferenzstatistik gewöhnt an feststellen, ob es einen signifikanten Unterschied zwischen den Mittelwerten zweier Gruppen gibt, der in bestimmten Merkmalen zusammenhängen kann. EIN T - Prüfung ist benutzt als eine Hypothese testen Werkzeug, das es ermöglicht testen einer Annahme, die auf eine Population anwendbar ist.
Die Leute fragen auch, wie berechnet man einen Einstichproben-t-Test?
Die ein stichprobe t test vergleicht den Mittelwert deiner Stichprobe Daten auf einen bekannten Wert. Zum Beispiel , möchten Sie vielleicht wissen, wie Sie Stichprobe Mittelwert vergleicht mit dem Bevölkerungsmittelwert.
Beispiel für einen T-Test mit einer Probe
- Der Stichprobenmittelwert (x¯).
- Der Bevölkerungsmittelwert (μ).
- Die Standardabweichung(en) der Stichprobe = 15 $.
- Anzahl der Beobachtungen(n) = 25.
Was ist ein AF-Test?
Ein F - Prüfung ist irgendeine Statistik Prüfung in dem die Prüfung Statistik hat ein F -Verteilung unter der Nullhypothese. Es wird am häufigsten beim Vergleich statistischer Modelle verwendet, die an einen Datensatz angepasst wurden, um das Modell zu identifizieren, das am besten zu der Population passt, aus der die Daten entnommen wurden.
Empfohlen:
Wie lautet die Formel für die Transformationseffizienz?
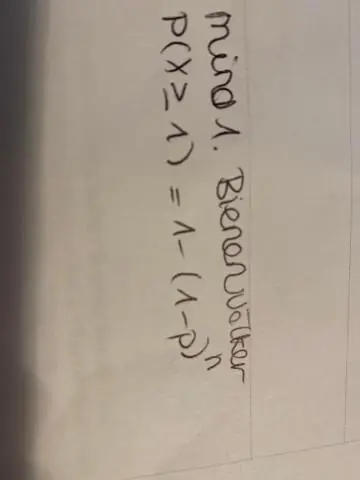
Sie kann berechnet werden, indem die Anzahl der erfolgreichen Transformanten durch die während eines Transformationsverfahrens verwendete DNA-Menge geteilt wird
Wie lautet die Formel für die Projektilbewegung?

Formeln für die Projektilbewegung. Ein Projektil ist ein Objekt, dem eine Anfangsgeschwindigkeit gegeben wird und auf das die Schwerkraft einwirkt. Geschwindigkeit ist ein Vektor (er hat Betrag und Richtung), daher kann die Gesamtgeschwindigkeit eines Objekts durch Vektoraddition der x- und y-Komponenten ermittelt werden: v2 = vx2 + vy2
Wie lautet die Formel für die maximale Höhe?

Wenn α = 0°, dann ist die vertikale Geschwindigkeit gleich 0 (Vy = 0), und das ist der Fall der horizontalen Projektilbewegung. Assine von 0° ist 0, dann verschwindet der zweite Teil der Gleichung und wir erhalten: hmax = h - die Anfangshöhe, von der aus wir das Objekt starten, ist die maximale Höhe in der Projektilbewegung
Wie lautet die Formel für die Division in Excel?

Um Zelle A2 durch Zelle B2 zu teilen: =A2/B2. Teilen Sie mehrere Zellen nacheinander auf, geben Sie Zellreferenzen ein, die durch das Teilungssymbol getrennt sind. Um beispielsweise die Zahl in A2 durch die Zahl in B2 zu teilen und dann das Ergebnis durch die Zahl in C2 zu teilen, verwenden Sie diese Formel: =A2/B2/C2
Wie lautet die Formel für den Krümmungsradius?

Der Krümmungsradius einer Kurve an einem Punkt M(x,y) wird als Kehrwert der Krümmung K der Kurve an diesem Punkt bezeichnet: R=1K. Daher ist für ebene Kurven, die durch die explizite Gleichung y=f(x) gegeben sind, der Krümmungsradius an einem Punkt M(x,y) durch den folgenden Ausdruck gegeben:R=[1+(y'(x))2]32| y''(x)
