
Inhaltsverzeichnis:
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:32.
- Zuletzt bearbeitet 2025-01-22 16:55.
Additionseigenschaft der Gleichheit
Wenn zwei Ausdrücke gleich sind und Sie auf beiden Seiten der Gleichung denselben Wert hinzufügen, bleibt die Gleichung gleich. Wenn du lösen eine Gleichung, finden Sie den Wert der Variablen, die die Gleichung wahr macht. Um zu lösen der Gleichung, isolieren Sie die Variable.
Was bedeutet demnach die Additionseigenschaft der Gleichheit?
Additionseigenschaft der Gleichheit . Die Eigentum Das besagt, dass, wenn Sie auf beiden Seiten einer Gleichung dieselbe Zahl hinzufügen, die Seiten gleich bleiben (d. h. die Gleichung ist weiterhin wahr.)
Welche Anweisung ist außerdem ein Beispiel für die Additionseigenschaft der Gleichheit? Die additive Eigenschaft der Gleichheit besagt, dass, wenn auf beiden Seiten einer Gleichung der gleiche Betrag addiert wird, die Gleichberechtigung ist immer noch wahr. Seien a, b und c reelle Zahlen, die aus rationalen Zahlen (z. B. 0, -7 und 2/3) und irrationalen Zahlen (z. B. Pi und der Quadratwurzel von 5) bestehen.
Ebenso wird gefragt, wie man Gleichheiten löst?
Zusammenfassung
- Viele einfache Ungleichungen lassen sich lösen, indem man beide Seiten addiert, subtrahiert, multipliziert oder dividiert, bis die Variable allein übrigbleibt.
- Aber diese Dinge werden die Richtung der Ungleichung ändern:
- Multiplizieren oder dividieren Sie nicht mit einer Variablen (es sei denn, Sie wissen, dass sie immer positiv oder immer negativ ist)
Was sind die 4 Eigenschaften der Gleichheit?
- Die reflexive Eigenschaft. a = a.
- Die symmetrische Eigenschaft. Wenn a=b, dann b=a.
- Die Übergangseigenschaft. Wenn a=b und b=c ist, dann ist a=c.
- Die Substitutionseigenschaft. Wenn a = b, dann kann b in jeder Gleichung durch a ersetzt werden.
- Die Additions- und Subtraktionseigenschaften.
- Die Multiplikationseigenschaften.
- Die Abteilungseigenschaften.
- Die Quadratwurzel-Eigenschaft*
Empfohlen:
Was bedeutet die Multiplikationseigenschaft der Gleichheit?

Multiplikationseigenschaft der Gleichheit. Die Multiplikationseigenschaft der Gleichheit besagt, dass, wenn Sie beide Seiten einer Gleichung mit derselben Zahl multiplizieren, die Seiten gleich bleiben (d. h. die Gleichheit bleibt erhalten)
Was ist die Eigenschaft der Gleichheit in der Mathematik?

Eigenschaften von Gleichheiten. Zwei Gleichungen, die die gleiche Lösung haben, werden äquivalente Gleichungen genannt, z.B. 5 + 3 = 2 + 6. Und dies, wie wir in einem vorherigen Abschnitt gelernt haben, wird durch das Gleichheitszeichen = angezeigt. Eine inverse Operation sind zwei Operationen, die sich gegenseitig rückgängig machen, z.B. Addition und Subtraktion oder Multiplikation und Division
Was ist die Additionseigenschaft?

Eigenschaften der Addition. Es gibt vier mathematische Eigenschaften, die eine Addition beinhalten. Die Eigenschaften sind die kommutativen, assoziativen, additiven Identitäts- und distributiven Eigenschaften. Kommutative Eigenschaft: Wenn zwei Zahlen addiert werden, ist die Summe unabhängig von der Reihenfolge der Addenden gleich. Zum Beispiel 4 + 2 = 2 +4
Wie löst man ein lineares Programmierproblem mit der Methode der Ecken?
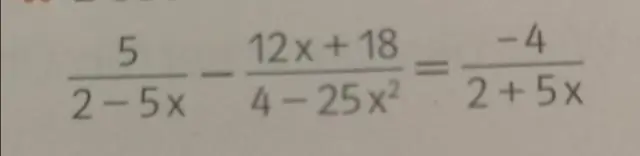
DIE METHODE DER ECKEN Zeichnen Sie die zulässige Menge (Region) S. Finden Sie die EXAKTen Koordinaten aller Eckpunkte (Eckpunkte) von S. Bewerten Sie die Zielfunktion P an jedem Eckpunkt Das Maximum (falls vorhanden) ist der größte Wert von P an einem Scheitelpunkt. Das Minimum ist der kleinste Wert von P an einer Ecke
Wie löst man eine Gleichung, indem man die Variable isoliert?
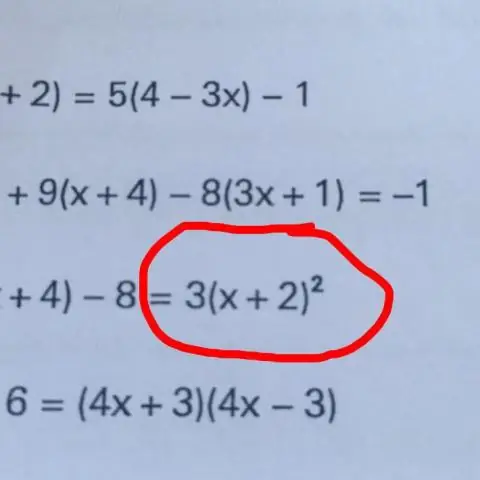
Die grundlegende Technik, eine Variable zu isolieren, besteht darin, „etwas auf beiden Seiten der Gleichung zu tun“, wie zum Beispiel Addieren, Subtrahieren, Multiplizieren oder Dividieren beider Seiten der Gleichung durch dieselbe Zahl. Durch Wiederholen dieses Vorgangs können wir die Variable auf einer Seite der Gleichung isoliert bekommen
