
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:32.
- Zuletzt bearbeitet 2025-01-22 16:55.
Chebyshevs Ungleichung sagt dass mindestens 1-1/K2 der Daten einer Stichprobe müssen innerhalb von K Standardabweichungen vom Mittelwert liegen (hier K ist jede positive reelle Zahl größer als eins). Aber wenn der Datensatz ist nicht glockenförmig verteilt, dann könnte ein anderer Betrag innerhalb einer Standardabweichung liegen.
Was misst dementsprechend die Ungleichung von Tschebyschew?
Tschebyschews Ungleichung (auch bekannt als Tchebysheffs Ungleichheit ) ist ein messen des Abstands vom Mittelwert eines zufälligen Datenpunkts in einer Menge, ausgedrückt als Wahrscheinlichkeit. Sie besagt, dass für einen Datensatz mit endlicher Varianz die Wahrscheinlichkeit, dass ein Datenpunkt innerhalb von k Standardabweichungen vom Mittelwert liegt, 1/k. beträgt2.
Und was ist die Satzformel von Chebyshev? Der Satz von Tschebyschew Zustände für jedes k > 1, mindestens 1-1/k2 der Daten liegt innerhalb von k Standardabweichungen vom Mittelwert. Wie bereits erwähnt, muss der Wert von k größer als 1 sein Formel und setzen Sie den Wert 2 ein, erhalten wir einen resultierenden Wert von 1-1/22, was 75% entspricht.
Wie beweist man unter Berücksichtigung dieser Tatsachen die Tschebyschew-Ungleichung?
Einer Möglichkeit, die Ungleichung von Chebyshev zu beweisen ist die Anwendung von Markovs Ungleichheit zur Zufallsvariablen Y = (X − Μ)2 mit a = (kσ)2. Tschebyschews Ungleichung dann folgt durch Division durch k2σ2.
Was ist der Satz von Chebyshev und wie wird er verwendet?
Der Satz von Tschebyschew ist Gebraucht um den Anteil der Beobachtungen zu finden, von dem Sie erwarten würden, dass er innerhalb von zwei Standardabweichungen vom Mittelwert liegt. Tschebyschews Intervall bezieht sich auf die Intervalle, die Sie finden möchten, wenn Sie das Satz . Ihr Intervall kann beispielsweise -2 bis 2 Standardabweichungen vom Mittelwert betragen.
Empfohlen:
Wie findet man die Achsenabschnitte einer Ungleichung?
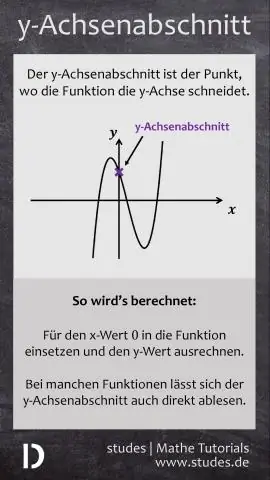
Alternativ können wir den x-Achsenabschnitt und den y-Achsenabschnitt der linearen Ungleichung der Standardform bestimmen, indem wir y = 0 einsetzen, dann nach x auflösen und x = 0 ersetzen, dann jeweils nach y auflösen. Denken Sie daran, dass der x-Achsenabschnitt der Wert von x ist, wenn y = 0 und der x-Achsenabschnitt der Wert von y ist, wenn x = 0
Wie schattiert man den Bereich einer Ungleichung?
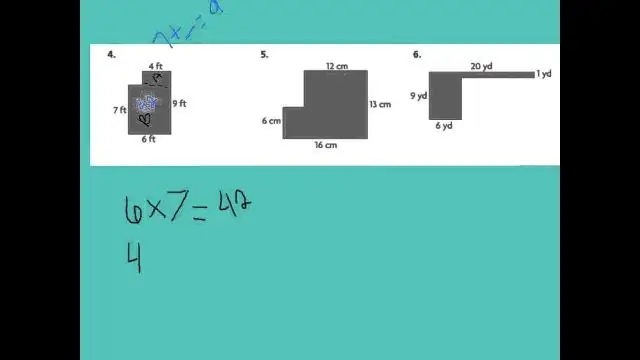
Es gibt drei Schritte: Ordne die Gleichung so um, dass 'y' links und alles andere rechts steht. Zeichnen Sie die 'y='-Linie (machen Sie eine durchgezogene Linie für y≤ oder y≥ und eine gestrichelte Linie für y) Schattieren Sie oberhalb der Linie für ein 'größer als' (y> oder y≥) oder unterhalb der Linie für a 'weniger als' (y< oder y≤)
Was sagt ein pH-Wert von 7 über einen Stoff aus?

PH: Definition und Maßeinheiten Der pH-Wert ist ein Maß dafür, wie sauer/basisch Wasser ist. Der Bereich reicht von 0 bis 14, wobei 7 neutral ist. pH-Werte von weniger als 7 weisen auf Säure hin, während ein pH-Wert von mehr als 7 auf eine Base hinweist. Der pH-Wert ist wirklich ein Maß für die relative Menge an freiem Wasserstoff und Hydroxylionen im Wasser
Was sagt die Struktur der DNA-Doppelhelix über die Eigenschaften der DNA aus?

Was sagt die Struktur der DNA-Doppelhelix über die Eigenschaften der DNA aus? DNA kann repliziert werden, indem komplementäre Kopien jedes Strangs hergestellt werden. Die DNA speichert genetische Informationen in der Reihenfolge ihrer Basen. DNA kann sich ändern
Was sagt die chemische Formel von Magnesiumchlorid über die Verbindung aus?

Die chemische Formel von Magnesiumchlorid ist _MgCl2. Da Magnesium zur 2. Gruppe im Periodensystem gehört und +2 Ion bildet und Chlor zur Halogenfamilie gehört und -1 Ion bildet. Sie reagieren also zu MgCl2. Magnesium verbindet sich mit 2 Cl-Atomen, um seine Oktate zu vervollständigen
