Inhaltsverzeichnis:
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:32.
- Zuletzt bearbeitet 2025-01-22 16:55.
Der Begriff zentrale Tendenz bezieht sich auf den mittleren oder typischen Wert einer Menge von Daten , was am häufigsten vorkommt gemessen unter Verwendung der drei ms: Mittelwert, Median und Modus. Mittelwert, Median und Modus werden als bezeichnet Maße der zentralen Tendenz.
Was ist auf diese Weise ein Maß für die zentrale Tendenz für gruppierte Daten?
Mittelwert, Median, Modus: Maße der zentralen Tendenz . Mittelwert für Gruppierte Daten Gruppierte Daten sind die Daten oder Scores, die in einer Häufigkeitsverteilung angeordnet sind.
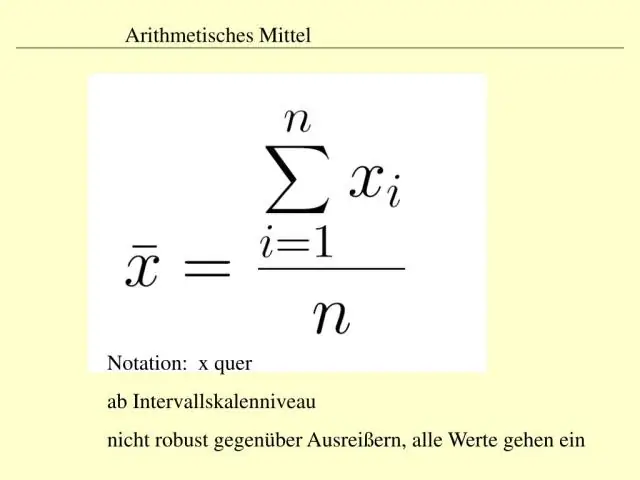
Wie lösen Sie den Mittelwert für nicht gruppierte Daten auf? Schritte
- Sammeln und zählen Sie Ihre Daten. Für jeden Satz von Datenwerten ist der Mittelwert ein Maß für den zentralen Wert.
- Finden Sie die Summe der Datenwerte. Der erste Schritt zur Ermittlung des Mittelwerts ist die Berechnung der Summe aller Datenpunkte.
- Teilen Sie, um den Mittelwert zu finden. Zum Schluss dividieren Sie die Summe durch die Anzahl der Werte.
Außerdem, welche Formel wird verwendet, um den mittleren Median und Modus für nicht gruppierte Daten zu ermitteln?
Zusammenfassung
- Für gruppierte Daten können wir den genauen Mittelwert, Median und Modus nicht finden, wir können nur Schätzungen geben.
- Um den Mittelwert zu schätzen, verwenden Sie die Mittelpunkte der Klassenintervalle: Geschätzter Mittelwert = Summe von (Mittelpunkt × Häufigkeit)Summe der Häufigkeit.
- Zur Schätzung der Median-Nutzung: Geschätzter Median = L + (n/2) − BG × w.
- Um die Modusnutzung abzuschätzen:
Wie lautet die Modusformel für gruppierte Daten?
Unser Lehrer erzählt a Formel herausfinden Modus , das heißt Z=L1+(F1-F0)/(2F1-F0-F2)*i wobei: L1 = untere Grenze der Modalklasse F1 = Modalklassenfrequenz. F2 = kurz nach der modalen Klassenfrequenz. F0 = kurz vor der modalen Klassenfrequenz.
Empfohlen:
Was sind nicht gruppierte Daten in Statistiken?
Nicht gruppierte Daten sind die Daten, die Sie zuerst aus einem Experiment oder einer Studie sammeln. Die Daten sind roh, d. h. sie sind nicht in Kategorien sortiert, klassifiziert oder anderweitig gruppiert. Ein nicht gruppierter Datensatz ist im Grunde eine Liste von Zahlen
Was ist der Unterschied zwischen der Masse eines Protons und der Masse eines Elektrons?
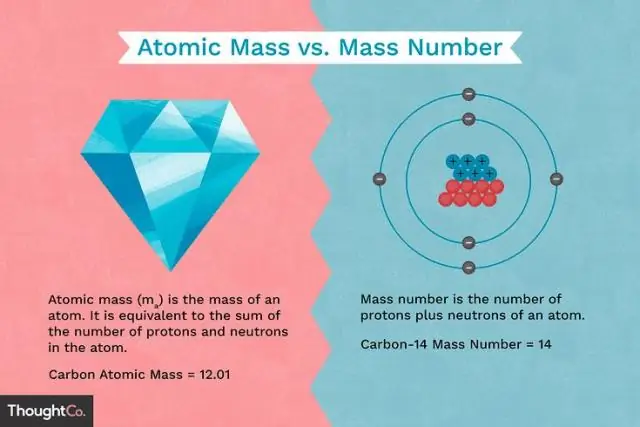
Protonen und Neutronen haben ungefähr die gleiche Masse, aber sie sind beide viel massiver als Elektronen (ungefähr 2.000 Mal so massiv wie ein Elektron). Die positive Ladung eines Protons ist betragsmäßig gleich der negativen Ladung eines Elektrons
Welche Eigenschaft von Daten ist ein Maß für den Wert, den die Daten sehr schätzen?
Variation: Ein Maß für den Betrag, um den die Datenwerte variieren. ? Verteilung: Die Art oder Form der Streuung der Daten über den Wertebereich (z. B. glockenförmig). ? Ausreißer: Sample-Werte, die sehr weit von der überwiegenden Mehrheit der anderen Sample-Werte entfernt liegen
Was sind die 10 zentralen Themen der Biologie?

Diese Links bilden die 10 Themen der Biologie. Emergente Eigenschaften. Das Leben existiert in hierarchischer Form, von einzelligen Bakterien bis hin zur gesamten Biosphäre mit all ihren Ökosystemen. Die Zelle. Erbliche Informationen. Struktur und Funktion. Umweltinteraktionen. Rückmeldung und Regulierung. Einheit und Vielfalt. Evolution
Inwiefern ist die Theorie des zentralen Ortes für Geographen nützlich?

Theorie des zentralen Ortes. Die zentrale Ortstheorie ist eine geographische Theorie, die versucht, die Anzahl, Größe und Lage menschlicher Siedlungen in einem Wohnsystem zu erklären. Es wurde 1933 eingeführt, um die räumliche Verteilung von Städten über die Landschaft zu erklären
