Inhaltsverzeichnis:
Video: Wie schreibt man eine unendliche Menge?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2024-01-18 08:12
Beispiele für unendliche Mengen:
- Satz aller Punkte in einer Ebene ist ein unendliche Menge .
- Satz aller Punkte in einem Liniensegment ist ein unendliche Menge .
- Satz aller positiven ganzen Zahlen, die ein Vielfaches von 3 ist, ist an unendliche Menge .
- W = {0, 1, 2, 3, ……..} d.h. einstellen aller ganzen Zahlen ist ein unendliche Menge .
- N = {1, 2, 3, ……….}
- Z = {………
In ähnlicher Weise können Sie sich fragen, wie Sie eine unendliche Menge zeigen können.
Sie können beweisen, dass eine Menge unendlich ist, indem Sie einfach zwei Dinge demonstrieren:
- Für ein gegebenes n hat es mindestens ein Element der Länge n.
- Wenn es ein Element maximaler endlicher Länge hat, können Sie ein längeres Element konstruieren (und damit ein Element maximaler endlicher Länge widerlegen).
Zweitens, wie erkennt man, ob eine Menge unendlich oder endlich ist? Punkte, um eine Menge als endlich oder unendlich zu bestimmen, sind:
- Wenn eine Menge sowohl einen Start- als auch einen Endpunkt hat, ist sie endlich, aber wenn sie keinen Start- oder Endpunkt hat, ist sie unendlich.
- Wenn eine Menge eine begrenzte Anzahl von Elementen hat, ist sie endlich, aber wenn ihre Anzahl von Elementen unbegrenzt ist, ist sie unendlich.
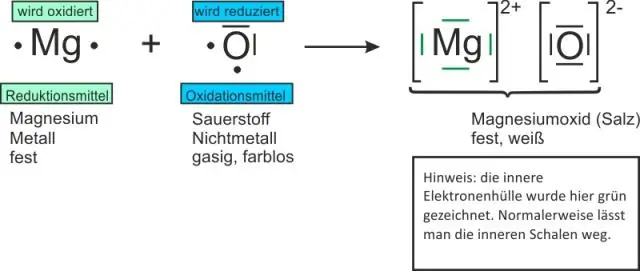
Zweitens, was ist endlich und unendlich mit Beispiel?
Beispiele von Unendliche Sätze Wenn eine einstellen ist kein endliche Menge , dann ist es ein unendliche Menge . Natürliche Zahlen und ganze Zahlen sind zwei Beispiele von Sätze das sind unendlich und daher nicht endlich . Das fett gedruckte Z wird oft verwendet, um die einstellen von ganzen Zahlen.
Gibt es unendliche Mengen?
Es gibt keine unendliche Mengen . Nicht nur mach unendlich viele sätze nicht existieren , aber das Konzept selbst ist logisch widersprüchlich – nicht anders als „quadratische Kreise“. Unendliche Sätze sind buchstäblich in den modernen Grundlagen der Mathematik verankert – mit dem sogenannten „Axiom of Unendlichkeit ”.
Empfohlen:
Wie schreibt man eine Koordinatenregel für eine Drehung?
Um eine Regel für diese Rotation zu schreiben, würdest du schreiben: R270? (x,y) = (−y,x). Notationsregel Eine Notationsregel hat die Form R180? A → O = R180? (x,y) → (−x,−y) und teilt Ihnen mit, dass das Bild A um den Ursprung gedreht wurde und sowohl die x- als auch die y-Koordinaten mit -1 . multipliziert werden
Wie schreibt man eine Funktionsregel für eine Eingabe-Ausgabe-Tabelle?
Jedes Zahlenpaar in der Tabelle ist durch dieselbe Funktionsregel verbunden. Diese Regel lautet: Multiplizieren Sie jede Eingabenummer (egin{align*}xend{align*}-Wert) mit 3, um die Ausgabenummer (egin{align*}yend{align*}-Wert) zu finden. Sie können eine solche Regel verwenden, um auch andere Werte für diese Funktion zu finden
Wie kann eine Gleichung unendliche Lösungen haben?
Eine lineare Gleichung hat unendlich viele Lösungen (in der Variablen x) genau dann, wenn beide Gesamtkoeffizienten von x auf beiden Seiten gleich sind und die Gesamtkonstanten auf beiden Seiten gleich sind
Wie schreibt man eine Gleichung in Form eines Steigungsabschnitts für eine Tabelle?
Nehmen Sie die Gleichung y = mx + b und setzen Sie den m-Wert (m = 1) und ein Paar von (x, y)-Koordinaten aus der Tabelle ein, z. B. (5, 3). Dann nach b auflösen. Verwenden Sie schließlich die gefundenen m- und b-Werte (m = 1 und b = -2), um die Gleichung zu schreiben
Welche Relation, die durch eine Menge geordneter Paare definiert wird, ist eine Funktion?
Eine Relation ist eine Menge geordneter Paare. DOMAN RANGE Page 2 Eine Funktion ist eine Relation, die jeden Wert in einem Set (dem Bereich) GENAU EINEM Wert in einem anderen Set (dem Bereich) zuweist. Die unabhängige Variable (oder Eingabe) repräsentiert willkürliche Werte in der Domäne