Video: Was ist der Zusammenhang von Statistik in der Wahrscheinlichkeit?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
Wahrscheinlichkeit und Statistiken sind verwandte Gebiete der Mathematik, die sich mit der Analyse der relativen Häufigkeit von Ereignissen befassen. Wahrscheinlichkeit befasst sich mit der Vorhersage der Wahrscheinlichkeit zukünftiger Ereignisse, während Statistiken beinhaltet die Analyse der Häufigkeit vergangener Ereignisse.
Welche Bedeutung haben dabei Statistik und Wahrscheinlichkeit?
Statistik und Wahrscheinlichkeit Theorie sind in der Medizin unabdingbar. Sie werden verwendet, um neue Medikamente zu testen und die Wahrscheinlichkeit zu ermitteln, dass Patienten Nebenwirkungen der Medikamente entwickeln. Tests werden an großen Tier- oder Personengruppen durchgeführt und Statistiken ist das Werkzeug, das benötigt wird, um die Tests auszuwerten.
Wie lautet die Wahrscheinlichkeitsformel für die Statistik? Formel für die Wahrscheinlichkeit von A und B (unabhängige Ereignisse): p(A und B) = p(A) * p(B). Wenn die Wahrscheinlichkeit eines Ereignisses das andere nicht beeinflusst, Sie haben ein unabhängiges Ereignis. Alles, was Sie tun, ist, die zu multiplizieren Wahrscheinlichkeit von einem von der Wahrscheinlichkeit eines anderen.
Was bedeuten Statistik und Wahrscheinlichkeit in diesem Zusammenhang?
Statistik und Wahrscheinlichkeit . Wahrscheinlichkeit ist das Studium des Zufalls und ist ein sehr grundlegendes Fach, das wir im täglichen Leben anwenden, während Statistiken beschäftigt sich mehr damit, wie wir mit Daten mithilfe verschiedener Analysetechniken und Erhebungsmethoden umgehen.
Was ist breiter zwischen Statistik und Wahrscheinlichkeit?
Statistiken ist die Wissenschaft, Entscheidungen unter Unsicherheit zu treffen. Statistiken Verwendet Wahrscheinlichkeit um das Vertrauen zu messen, das man in diese Entscheidungen hat. Wahrscheinlichkeit ist die Mathematik des erwarteten Verhaltens zufälliger Ereignisse. EIN statistisch Der Test wird aus Beispieldaten berechnet (z. B. der t-Test eines Schülers).
Empfohlen:
Wie ist der Zusammenhang zwischen Struktur und Funktion?
In der Biologie ist eine Schlüsselidee, dass die Struktur die Funktion bestimmt. Mit anderen Worten, die Art und Weise, wie etwas angeordnet ist, ermöglicht es ihm, seine Rolle zu spielen, seine Aufgabe innerhalb eines Organismus (eines Lebewesens) zu erfüllen. Struktur-Funktions-Beziehungen entstehen durch den Prozess der natürlichen Selektion
Was ist der funktionelle Zusammenhang zwischen den Nukleolus-Kernporen und der Kernmembran?
Welcher funktionelle Zusammenhang besteht zwischen dem Nukleolus, den Kernporen und der Kernmembran? A. Der Nukleolus enthält Boten-RNA (mRNA), die die Kernhülle durch die Kernporen durchquert
Was ist der Unterschied zwischen bedingter Wahrscheinlichkeit und gemeinsamer Wahrscheinlichkeit?
Im Allgemeinen ist die gemeinsame Wahrscheinlichkeit die Wahrscheinlichkeit, dass zwei Dinge* zusammen passieren: z. B. die Wahrscheinlichkeit, dass ich mein Auto wasche und es regnet. Bedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit, dass etwas passiert, vorausgesetzt, dass das andere passiert: z. B. die Wahrscheinlichkeit, dass es regnet, wenn ich mein Auto wasche
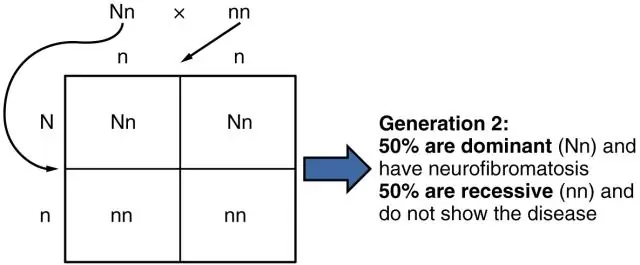
Warum ist es wichtig, dass die Wahrscheinlichkeit in der Mendelschen Genetik berechnet werden kann?
In der Genetik kann die theoretische Wahrscheinlichkeit verwendet werden, um die Wahrscheinlichkeit zu berechnen, dass Nachkommen ein bestimmtes Geschlecht haben oder dass Nachkommen ein bestimmtes Merkmal oder eine bestimmte Krankheit erben, wenn alle Ergebnisse gleich möglich sind. Es kann auch verwendet werden, um Wahrscheinlichkeiten von Merkmalen in größeren Populationen zu berechnen
Wie hoch ist die Wahrscheinlichkeit, dass der Yellowstone ausbricht?
Die USGS schätzt die Wahrscheinlichkeit auf 1 zu 730.000 in einem bestimmten Jahr. Es besteht auch eine gute Chance, dass die Verschiebung der tektonischen Platten in Nordamerika die Wahrscheinlichkeit einer Eruption vollständig beseitigt hat, indem der Magma-Hotspot unter Yellowstone gezwungen wurde, auf kältere, energiefressende Gesteine zu treffen