Inhaltsverzeichnis:
Video: Wie schreibt man einen Bruch als Produkt einer ganzen Zahl und einem Einheitsbruch?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:33
Regeln zum Ermitteln des Produkts eines Einheitsbruchs und einer ganzen Zahl
- Wir zuerst schreiben das ganze Zahl Als ein Fraktion , d.h., Schreiben es geteilt durch eins; Beispiel: 7 wird als 71 geschrieben.
- Dann multiplizieren wir die Zähler.
- Wir multiplizieren die Nenner.
- Wenn eine Vereinfachung erforderlich ist, wird sie durchgeführt und dann wir schreiben der endgültige Fraktion .
Welche Regel können Sie vor diesem Hintergrund schreiben, um eine ganze Zahl durch einen Einheitsbruch zu teilen?
Ja, wenn Dividieren einer ganzen Zahl durch einen Einheitsbruch , multiplizieren die ganze Zahl bis zum Einheitsbruch Nenner geht immer! ein geteilt um (1/b) = a mal (b/1) = (a/1) mal (b/1) = ab/1 = ab.
Wissen Sie auch, was der Wert von 1 Einheit als Bruch ist? EIN Einheitsbruch ist eine rationale Zahl geschrieben als a Fraktion wo der Zähler ist einer und der Nenner ist eine positive ganze Zahl. EIN Einheitsbruch ist also der Kehrwert einer positiven ganzen Zahl, 1 /n. Beispiele sind 1 / 1 , 1 /2, 1 /3, 1 /4, 1 /5 usw.
Die Leute fragen auch, was ist das Produkt in einer Fraktion?
EIN Fraktion muss vereinfacht werden, wenn die gleiche Zahl sowohl den Zähler als auch den Nenner von a divide teilen kann Fraktion . Aus 4/6 würde also 2/3 werden und Sie würden mit 3/5 multiplizieren. Multiplizieren Sie die Zähler. Multipliziere die oberste Zahl mit einem Fraktion durch die oberste Zahl im anderen Fraktion.
Wie finde ich das Produkt?
Die Produkt ist die Antwort auf ein Multiplikationsproblem. Sie finden a Produkt durch einen Vorgang, der wiederholte Addition genannt wird, d. h. indem die Anzahl der Gruppen in der Aufgabe zusammengezählt wird.
Empfohlen:
Was ist das Produkt einer ganzen Zahl?
Regel 1: Das Produkt einer negativen ganzen Zahl und einer positiven ganzen Zahl ist eine negative ganze Zahl. Regel 2: Das Produkt von zwei positiven ganzen Zahlen oder zwei negativen ganzen Zahlen ist eine positive ganze Zahl. Das heißt, wenn Sie zwei OF gleichen Vorzeichenzahlen multiplizieren, ist das Produkt immer positiv. GLEICH
Wie schreibt man 13/4 als gemischte Zahl?
Als negativer unechter Bruch (|Zähler| > |Nenner|): - 13/4 = - 13/4 Als gemischte Zahl. (eine ganze Zahl und ein echter Bruch mit gleichem Vorzeichen): - 13/4 = - 3 1/4 In Prozent: - 13/4 = - 325 %
Wie schreibt man als Bruch in einfachster Form?
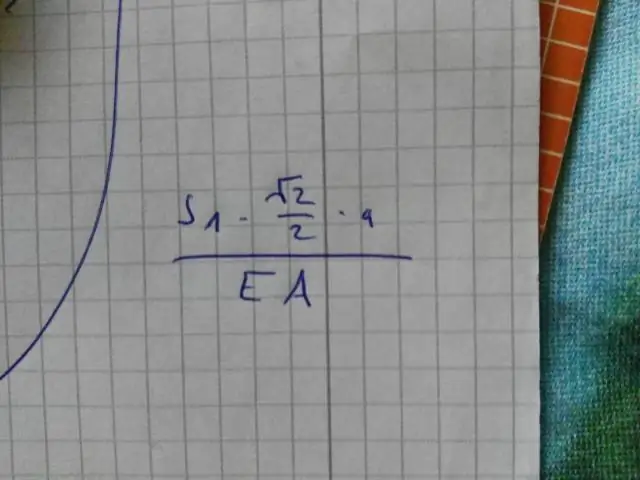
Beim Schreiben von Brüchen in einfachster Form sind zwei Regeln zu beachten: Fragen Sie, ob Zähler und Nenner durch dieselbe Zahl geteilt werden können, die als gemeinsamer Faktor bezeichnet wird. Prüfen Sie, ob mindestens eine Zahl im Bruch eine Primzahl ist
Wie hängt die Subtraktion von ganzen Zahlen mit der Addition von ganzen Zahlen zusammen?
Antwort und Erklärung: Das Addieren von ganzen Zahlen bedeutet das Addieren von ganzen Zahlen mit gleichen Vorzeichen, während das Subtrahieren von ganzen Zahlen das Addieren der ganzen Zahlen mit entgegengesetzten Vorzeichen bedeutet
Wie wird die Größe einer Zahl geändert, wenn Sie mit einem Bruch multiplizieren?
Antwort: Skalierung ist der Prozess der Größenänderung einer Zahl um einen Bruch, der größer oder kleiner als 1 . ist