Inhaltsverzeichnis:
Video: Was sind die Annahmen der linearen Programmierung?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
Annahmen der linearen Programmierung
- Bedingungen der Gewissheit. Es bedeutet, dass Zahlen in der Zielsetzung und Einschränkungen sind mit Sicherheit bekannt und ändern sich während des Untersuchungszeitraums.
- Linearität oder Proportionalität.
- Additiv.
- Teilbarkeit.
- Nicht negative Variable.
- Endlichkeit.
- Optimalität.
Anschließend kann man sich auch fragen, welche der folgenden Grundannahmen der linearen Programmierung zugrunde liegen?
Der Zustand der Unsicherheit existiert. Unabhängigkeit besteht für die Aktivitäten. Verhältnismäßigkeit existiert in der objektiven Funktion und in den Beschränkungen.
Was sind die Komponenten der linearen Programmierung? Es besteht aus vier grundlegenden Komponenten : Entscheidungsvariablen repräsentieren zu bestimmende Größen. Die Zielfunktion stellt dar, wie sich die Entscheidungsvariablen auf die zu optimierenden Kosten oder den zu optimierenden Wert (minimiert oder maximiert) auswirken.
Vor diesem Hintergrund, was sind die Annahmen und Grenzen der linearen Programmierung?
Annahmen und Einschränkungen bei der linearen Programmierung
- Es gibt eine Reihe von Beschränkungen oder Beschränkungen, die quantitativ ausgedrückt werden können.
- Die Parameter unterliegen Größenschwankungen.
- Die durch Beschränkungen und die Zielfunktionen ausgedrückten Beziehungen sind linear.
- Die Zielfunktion soll bzgl. die Variablen, die an dem Phänomen beteiligt sind.
Was ist Teilbarkeit in der linearen Programmierung?
Teilbarkeit - Die Entscheidungsvariablen können in nicht ganzzahlige Werte unterteilt werden, wobei Bruchwerte angenommen werden. Ganze Zahl Programmierung Techniken können verwendet werden, wenn die Teilbarkeit Annahme gilt nicht.
Empfohlen:
Was bedeutet Lambda in der linearen Algebra?
Es bedeutet, dass Sie eine Matrix nehmen, auf einen Vektor wirken lassen und den Vektor mit einer Skalarzahl davor zurückgeben
Welche Annahmen liegen der Lincoln-Petersen-Methode zugrunde?
Grundannahmen des Lincoln-Petersen-Schätzers: Die Population ist geschlossen (geografisch und demografisch). Alle Tiere werden in jeder Probe mit gleicher Wahrscheinlichkeit gefangen. Fangen und Markieren haben keinen Einfluss auf die Fangbarkeit
Was ist lineare Regression in der R-Programmierung?
Die lineare Regression wird verwendet, um den Wert einer kontinuierlichen Variablen Y basierend auf einer oder mehreren Eingabeprädiktorvariablen X vorherzusagen. Das Ziel besteht darin, eine mathematische Formel zwischen der Antwortvariablen (Y) und den Prädiktorvariablen (Xs) zu erstellen. Sie können diese Formel verwenden, um Y vorherzusagen, wenn nur X-Werte bekannt sind
Was ist die Simplex-Methode für die lineare Programmierung?
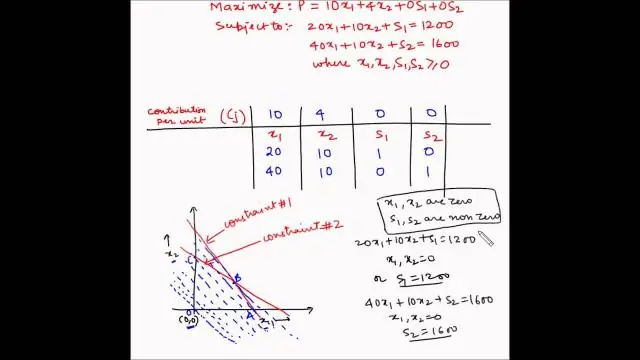
Simplex-Methode. Simplex-Methode, Standardtechnik in der linearen Programmierung zum Lösen eines Optimierungsproblems, typischerweise eines mit einer Funktion und mehreren als Ungleichungen ausgedrückten Nebenbedingungen. Die Ungleichungen definieren einen polygonalen Bereich (siehe Polygon), und die Lösung liegt typischerweise an einem der Eckpunkte
Was ist die Normalgleichung bei der linearen Regression?
Die Normalgleichung ist ein analytischer Ansatz für die lineare Regression mit einer Kostenfunktion der kleinsten Quadrate. Wir können den Wert von &thgr; ohne Gradient Descent zu verwenden. Dieser Ansatz ist eine effektive und zeitsparende Option, wenn Sie mit einem Datensatz mit kleinen Funktionen arbeiten