Inhaltsverzeichnis:
- Die Neigungsabschnittsform wird verwendet, wenn Ihre lineare Gleichung in der Form geschrieben wird:
Video: Wie findet man die Steigung mit Achsenabschnitten?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
Neigung - abfangen form ist y = mx + b form, wobei m die Neigung , und b steht für sie- abfangen . Wenn also die Gleichung einer Geraden y = 3/4 x - 2 ist, dann wird die Gerade geschrieben in Neigungsabschnitt Form oder y = mx+ b Form, mit m = 3/4 und b = -2.
Wie findet man in diesem Zusammenhang die Steigung in Form des Steigungsabschnitts?
y = 5x + 3 ist ein Beispiel für die Steigungsschnittform und vertritt die Gleichung einer Linie mit a Neigung von 5 und und ein y- abfangen von 3. y = −2x+ 6 steht für Gleichung einer Linie mit a Neigung von −2 und und ein y- abfangen von 6.
Man kann sich auch fragen, was ist die Steigungsformel? Um die zu berechnen Neigung einer Linie benötigen Sie nur zwei Punkte von dieser Linie, (x1, y1) und (x2, y2). Die Gleichung zur Berechnung der Neigung aus zwei Punkten ist: Auf einem Graphen kann dies dargestellt werden als: Es gibt drei Schritte bei der Berechnung von Neigung einer geraden Linie, wenn Ihnen ihre Gleichung nicht gegeben wird.
Die Frage ist auch, wie man eine Steigungsabschnittsgleichung grafisch darstellt?
Die Neigungsabschnittsform wird verwendet, wenn Ihre lineare Gleichung in der Form geschrieben wird:
- y = mx + b.
- Zeichnen Sie die Gleichung: y = 2x + 4.
- Steigung = 2 oder 2/1.
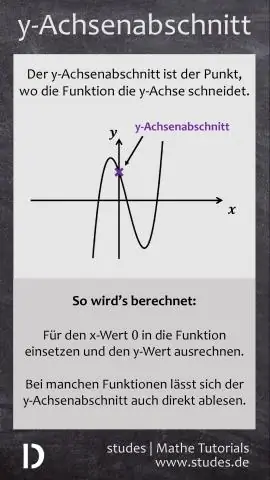
- Y-Achsenabschnitt = 4 oder (0, 4)
- Schritt 1: Zeichnen Sie den y-Achsenabschnitt in Ihr Diagramm ein.
- Schritt 2: Verwenden Sie vom y-Achsenabschnitt (0, 4) die Steigung, um Ihren nächsten Punkt zu zeichnen.
Wie findet man Steigung?
Die Neigung einer Linie kennzeichnet die Richtung einer Linie. Um die zu finden Neigung , dividieren Sie die Differenz der y-Koordinaten von 2 Punkten auf einer Linie durch die Differenz der x-Koordinaten dieser beiden Punkte.
Empfohlen:
Wie findet man die Durchschnittsgeschwindigkeit mit zwei Geschwindigkeiten?
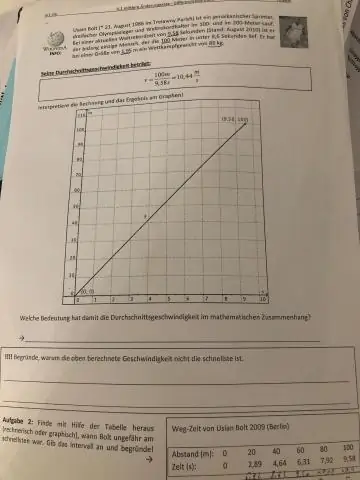
Die Summe aus Anfangs- und Endgeschwindigkeit wird durch 2 geteilt, um den Durchschnitt zu ermitteln. Der Durchschnittsgeschwindigkeitsrechner verwendet die Formel, die zeigt, dass die Durchschnittsgeschwindigkeit (v) gleich der Summe der Endgeschwindigkeit (v) und der Anfangsgeschwindigkeit (u) ist, geteilt durch 2
Wie findet man mit Pythagoras die gegenüberliegende Seite eines Dreiecks?
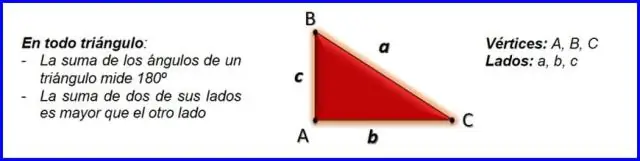
Rechtwinklige Dreiecke und der Satz des Pythagoras Der Satz des Pythagoras, a2+b2=c2, a 2 + b 2 = c 2, kann verwendet werden, um die Länge einer beliebigen Seite eines rechtwinkligen Dreiecks zu bestimmen. Die dem rechten Winkel gegenüberliegende Seite wird Hypotenuse genannt (Seite c in der Abbildung)
Wie findet man Steigung für Dummies?
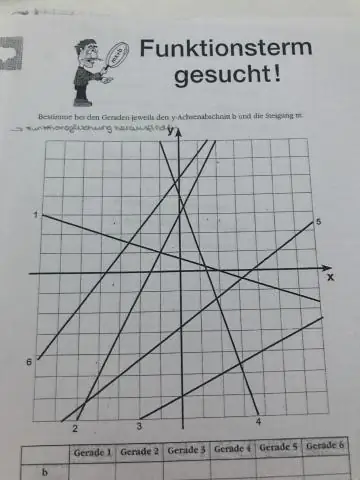
Dinge, die Sie sich merken sollten Steigung = Änderung von y gegenüber der Änderung von x. Steigung = (y2 - y1)/(x2 - x1) Steigung = Anstieg über Lauf. Sie können zwei beliebige Punkte auf einer Linie auswählen, um die Steigung zu berechnen. Sie können Ihre Antwort überprüfen, indem Sie verschiedene Punkte auf der Linie ausprobieren. Wenn die Linie von links nach rechts nach oben geht, ist die Steigung positiv
Wie findet man die Oberfläche einer Pyramide mit einem Netz?
VIDEO Wie groß ist die Gesamtoberfläche einer Pyramide? Die Oberfläche einer Pyramide Wenn alle Seitenflächen gleich sind: [Basis Bereich ] + 1 / 2 × Umfang × [schräge Länge] Man kann sich auch fragen, wie man die Oberfläche einer Kugel findet.
Wie findet man die Steigung einer parallelen und senkrechten Linie?
Um die Steigung dieser Geraden zu finden, müssen wir die Gerade in die Steigungsabschnittsform (y = mx + b) bringen, was bedeutet, dass wir nach y auflösen müssen: Die Steigung der Geraden 4x – 5y = 12 ist m = 4/ 5. Daher müsste die Steigung jeder Geraden parallel zu dieser Geraden m = 4/5 sein. Zwei Geraden stehen senkrecht, wenn