Inhaltsverzeichnis:
Video: Was ist die Umkehrfunktion in der Analysis?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
In der Mathematik und Umkehrfunktion (oder Anti- Funktion ) ist ein Funktion das "umkehrt" einen anderen Funktion : wenn die Funktion f angewendet auf eine Eingabe x ergibt ein Ergebnis von y, dann Anwendung seiner Umkehrfunktion g zu y ergibt das Ergebnis x und umgekehrt, d. h. f(x) = y genau dann, wenn g(y) = x.
Wie findet man folglich die Inverse einer Funktion in der Infinitesimalrechnung?
Die Umkehrung einer Funktion finden
- Ersetze zunächst f(x) durch y.
- Ersetze jedes x durch ein y und ersetze jedes y durch ein x.
- Löse die Gleichung aus Schritt 2 nach y auf.
- Ersetze y durch f−1(x) f − 1 (x).
- Überprüfen Sie Ihre Arbeit, indem Sie prüfen, dass (f∘f−1)(x)=x (f ∘ f − 1) (x) = x und (f−1∘f)(x)=x (f − 1 ∘ f) (x) = x sind beide wahr.
Was ist ein inverses Funktionsbeispiel? Umkehrfunktionen , im allgemeinsten Sinne, sind Funktionen die sich gegenseitig "umkehren". Zum Beispiel , wenn f a zu b nimmt, dann ist die invers , f − 1 f^{-1} f−1f, start hochgestellt, minus, 1, end hochgestellt, muss b zu a bringen.
Wie unterscheidet man hier inverse Funktionen?
Ableitungen von inversen trigonometrischen Funktionen
- Verwenden Sie den Umkehrfunktionssatz, um die Ableitung von g(x)=sin−1x zu bestimmen.
- Da für x im Intervall [−π2, π2] f(x)=sinx die Inverse von g(x)=sin−1x ist, suchen Sie zunächst f′(x).
- f′(x)=cosx.
- f′(g(x))=cos(sin−1x)=√1−x2.
- g′(x)=ddx(sin−1x)=1f′(g(x))=1√1−x2.
Was ist eine selbstinverse Funktion?
EIN selbstinverse Funktion ist ein Funktion f, mit y=f(x), mit der besonderen Eigenschaft, dass ff(x)=x, oder anders geschrieben, f(x)=f−1(x)
Empfohlen:
Hat eine kubische Funktion eine Umkehrfunktion?
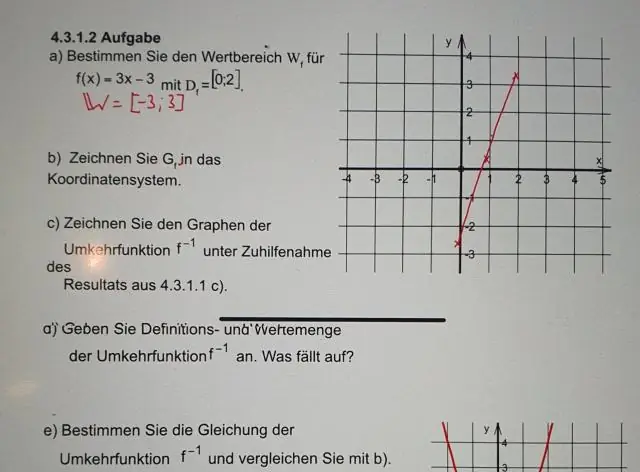
ALLGEMEIN hat KEINE INVERSE, WENN ES KEINE EINS-ZU-EINS-FUNKTION IST, weil nur solche Funktionen invertierbar sind. ? ABER wenn eine kubische Funktionis die folgende Form hat/in die folgende Form umgewandelt werden kann, ist sie invertierbar: (i) f(x)=(ax+b)³+c, a≠0, b,c'isin;|R , mit seiner natürlichen Domäne x&|R oder einer reduzierten Domäne
Was ist eine stetige Funktion in der Analysis?
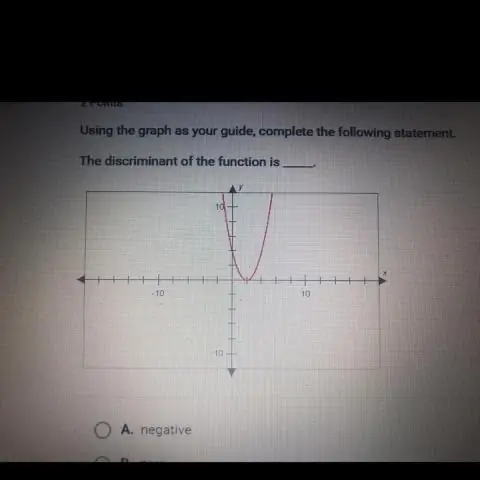
Wenn eine Funktion bei jedem Wert in einem Intervall stetig ist, dann sagen wir, dass die Funktion in diesem Intervall stetig ist. Und wenn eine Funktion in einem beliebigen Intervall stetig ist, nennen wir sie einfach eine stetige Funktion. In der Infinitesimalrechnung geht es im Wesentlichen um Funktionen, die bei jedem Wert in ihren Domänen stetig sind
Wer war der Genetiker, der für die Anwendung der DNA-Wissenschaft auf die Forensik verantwortlich ist?
Alec Jeffreys
Was ist eine zusammengesetzte Funktion in der Analysis?
Das Kombinieren von zwei (oder mehr) Funktionen wie dieser wird als Zusammensetzen der Funktionen bezeichnet, und die resultierende Funktion wird als zusammengesetzte Funktion bezeichnet. Die zusammengesetzte Funktionsregel zeigt uns einen schnelleren Weg. Regel 7 (Die zusammengesetzte Funktionsregel (auch bekannt als Kettenregel)) Wenn f(x) = h(g(x)) dann f (x) = h (g(x)) × g (x)
Was ist der Unterschied zwischen der räumlichen Perspektive und der ökologischen Perspektive in der Geographie?
Was ist der Unterschied zwischen der ökologischen Perspektive und der räumlichen Perspektive in der Geographie? die räumliche Perspektive ist, wo etwas passiert oder wo etwas ist. die ökologische Perspektive ist die Wechselwirkung zwischen den Dingen in der Umwelt