
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:32.
- Zuletzt bearbeitet 2025-01-22 16:55.
In der Mathematik, a Gruppe ist eine Menge, die mit einer binären Operation ausgestattet ist, die zwei beliebige Elemente zu einem dritten Element so kombiniert, dass vier Bedingungen genannt werden Gruppe Axiome sind erfüllt, nämlich Abschluss, Assoziativität, Identität und Invertibilität. Gruppen teilen eine grundlegende Verwandtschaft mit dem Begriff der Symmetrie.
Was ist in diesem Zusammenhang eine Gruppe und ihre Eigenschaften?
EIN Gruppe ist eine endliche oder unendliche Menge von Elementen zusammen mit einer binären Operation (genannt die Gruppe Operation), die zusammen die vier fundamentalen Eigenschaften der Geschlossenheit, Assoziativität, der Identität Eigentum , und das Gegenteil Eigentum.
Zweitens, was sind Gruppen in der abstrakten Algebra? Definition. EIN Gruppe (G, ·) ist eine nichtleere Menge G zusammen mit einer binären Operation · auf G, so dass folgende Bedingungen gelten: (i) Abschluss: Für alle a, b G ist das Element a · b ein eindeutig definiertes Element von G. (ii) Assoziativität: Für alle a, b, c gilt G. a · (b · c) = (a · b) · c.
Auch zu wissen, WAS IST Gruppe in der linearen Algebra?
In der Mathematik, a lineare algebraische Gruppe ist eine Untergruppe der Gruppe von invertierbaren n×n Matrizen (unter Matrix Multiplikation), die durch Polynomgleichungen definiert ist. Viele lügen Gruppen kann angesehen werden als lineare algebraische Gruppen über dem Körper der reellen oder komplexen Zahlen.
Was macht eine Gruppe zu einer Gruppe?
EIN Gruppe ist eine Ansammlung von Individuen, die Beziehungen zueinander haben, die sie in erheblichem Maße voneinander abhängig machen. So definiert ist der Begriff Gruppe bezieht sich auf eine Klasse von sozialen Einheiten, die die Eigenschaft der Interdependenz zwischen ihren konstituierenden Mitgliedern gemeinsam haben.
Empfohlen:
Was ist der Unterschied zwischen Algebra 1 und Algebra 2?

Der Hauptfokus von Algebra 1 ist das Lösen von Gleichungen. Die einzigen Funktionen, die Sie ausführlich betrachten werden, sind linear und quadratisch. Algebra 2 ist viel fortgeschrittener
Was ist der Trend der Elektronegativität nach unten in einer Gruppe?
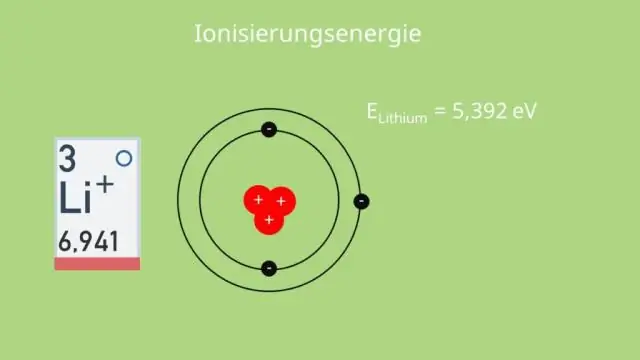
Wenn Sie sich also eine Gruppe im Periodensystem nach unten bewegen, nimmt die Elektronegativität eines Elements ab, da die erhöhte Anzahl von Energieniveaus die äußeren Elektronen sehr weit von der Anziehungskraft des Kerns entfernt. Die Elektronegativität nimmt zu, wenn Sie sich über eine Periode im Periodensystem von links nach rechts bewegen
Was ist der natürliche Prozess, der dazu führt, dass sich eine Gesteinsart in eine andere verwandelt?

Die drei Hauptgesteinsarten sind magmatisch, metamorph und sedimentär. Die drei Prozesse, die ein Gestein in ein anderes verwandeln, sind Kristallisation, Metamorphose sowie Erosion und Sedimentation. Jedes Gestein kann sich in jedes andere Gestein verwandeln, indem es einen oder mehrere dieser Prozesse durchläuft. Dadurch entsteht der Gesteinskreislauf
WAS IST Gruppe in der linearen Algebra?

Eine Gruppe ist eine endliche oder unendliche Menge von Elementen zusammen mit einer binären Operation (Gruppenoperation genannt), die zusammen die vier fundamentalen Eigenschaften der Schließung, Assoziativität, Identitätseigenschaft und inverse Eigenschaft erfüllen
Was sind eine Gruppe von Zellen, die eine gemeinsame Funktion erfüllen?

Gewebe sind Gruppen ähnlicher Zellen, die eine gemeinsame Funktion haben. Ein Organ ist eine Struktur, die aus mindestens zwei oder mehr Gewebearten besteht und eine bestimmte Reihe von Funktionen für den Körper erfüllt. Viele Organe, die zusammenarbeiten, um einen gemeinsamen Zweck zu erfüllen, werden als Organsystem bezeichnet
