Video: Gibt es eine Abschlusseigenschaft der Subtraktion, die für ganze Zahlen gilt?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
Schließung ist eine mathematische Eigentum in Beziehung stehende Sätze von Zahlen und Operationen. Wenn die Operation auf zwei Zahlen im Set ergibt a Nummer was im Set enthalten ist, haben wir Schließung . Wir haben festgestellt, dass die Menge von ganze Zahlen ist nicht geschlossen unter Subtraktion , aber die Menge der ganzen Zahlen ist abgeschlossen unter Subtraktion.
Gibt es hiervon eine Abschlusseigenschaft der Subtraktion?
Schließungseigenschaft Wenn eine ganze Zahl von einer anderen abgezogen wird, das Die Differenz ist nicht immer eine ganze Zahl. Dies bedeutet, dass das ganze Zahlen sind nicht geschlossen unter Subtraktion.
Und was bedeutet es, unter Subtraktion geschlossen zu sein? Schließung ist, wenn eine Operation (wie "Addieren") an Mitgliedern einer Menge (wie "Reelle Zahlen") immer macht Mitglied der gleichen Menge. Das Ergebnis bleibt also im selben Set.
Ebenso wird gefragt, ob die Subtraktion für ganze Zahlen geschlossen ist?
Ganze Zahlen : Dieses Set ist abgeschlossen nur unter Addition und Multiplikation. Ganzzahlen: Dieser Satz ist abgeschlossen nur unter Zusatz, Subtraktion und Multiplikation. Rational Zahlen : Dieses Set ist abgeschlossen unter zusätzlich, Subtraktion , Multiplikation und Division (mit Ausnahme der Division durch 0).
Was ist ein Beispiel für eine Verschlusseigenschaft?
Schließungseigenschaft . Die Verschlusseigenschaft bedeutet, dass eine Menge für eine mathematische Operation abgeschlossen ist. Zum Beispiel , die Menge der geraden natürlichen Zahlen, [2, 4, 6, 8,…], ist in Bezug auf die Addition abgeschlossen, weil die Summe zweier von ihnen eine weitere gerade natürliche Zahl ist, die ebenfalls ein Mitglied der Menge ist.
Empfohlen:
Sind ganze Zahlen immer manchmal oder nie rationale Zahlen?
1.5 ist eine rationale Zahl, die wie folgt geschrieben werden kann: 3/2 wobei 3 und 2 beide ganze Zahlen sind. Hier ist die rationale Zahl 8 eine ganze Zahl, aber die rationale Zahl 1,5 ist keine ganze Zahl, da 1,5 keine ganze Zahl ist. Wir können also sagen, dass eine rationale Zahl manchmal nicht immer eine ganze Zahl ist. Daher ist die richtige Antwort manchmal
Welche Arten von Zahlen bilden die Menge der Zahlen, die als reelle Zahlen bezeichnet werden?
Reelle Zahlenmengen (positive ganze Zahlen) oder die ganzen Zahlen {0, 1, 2, 3,} (die nicht negativen ganzen Zahlen). Mathematiker verwenden in beiden Fällen den Begriff „natürlich“
Was sind natürliche Zahlen, ganze Zahlen, ganze Zahlen und rationale Zahlen?
Reelle Zahlen werden hauptsächlich in rationale und irrationale Zahlen eingeteilt. Rationale Zahlen umfassen alle ganzen Zahlen und Brüche. Alle negativen ganzen und ganzen Zahlen bilden die Menge der ganzen Zahlen. Ganze Zahlen bestehen aus allen natürlichen Zahlen und Null
Wie hängt die Subtraktion von ganzen Zahlen mit der Addition von ganzen Zahlen zusammen?
Antwort und Erklärung: Das Addieren von ganzen Zahlen bedeutet das Addieren von ganzen Zahlen mit gleichen Vorzeichen, während das Subtrahieren von ganzen Zahlen das Addieren der ganzen Zahlen mit entgegengesetzten Vorzeichen bedeutet
Sind einige irrationale Zahlen ganze Zahlen?
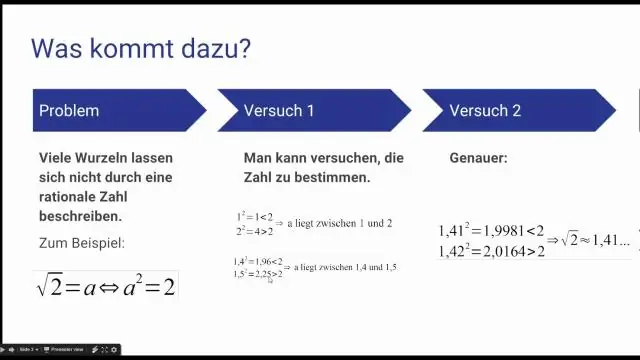
Antwort und Erklärung: Irrationale Zahlen sind keine ganzen Zahlen. Eine irrationale Zahl ist eine Zahl, die nicht rational ist. Mit anderen Worten, eine irrationale Zahl kann nicht geschrieben werden