
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:32.
- Zuletzt bearbeitet 2025-01-22 16:55.
Irrationale Zahlen wurden eingeführt, weil sie alles viel einfacher machen. Ohne irrationale Zahlen Wir haben nicht das Kontinuum des Realen Zahlen , was Geometrie und Physik und Technik entweder schwieriger oder schlichtweg unmöglich macht.
Wie werden auf diese Weise irrationale Zahlen im Alltag verwendet?
Eine der praktischsten Anwendungen von irrationale Zahlen findet den Umfang eines Kreises. C = 2πr Verwendet das irrationale Zahl ≈ 3.14159 5. pi=3.141592654 Personen Verwendet es beschäftigt sich mit Kreis, Kugel, Computergenauigkeit überprüfen.
Anschließend stellt sich die Frage, warum irrationale Zahlen unendlich sind. Es gibt eine Unendliche Nummer von irrationale Zahlen genauso wie es ein. gibt Unendliche Nummer von ganzen Zahlen, rational Zahlen und echt Zahlen . Da jedoch reelle Zahlen abzählbar und rationale abzählbar sind, sind Irrationale abzählbar, was bedeutet, dass es viel mehr irrationale als rationale gibt.
Wissen Sie auch, warum ich rationale und irrationale Zahlen brauche?
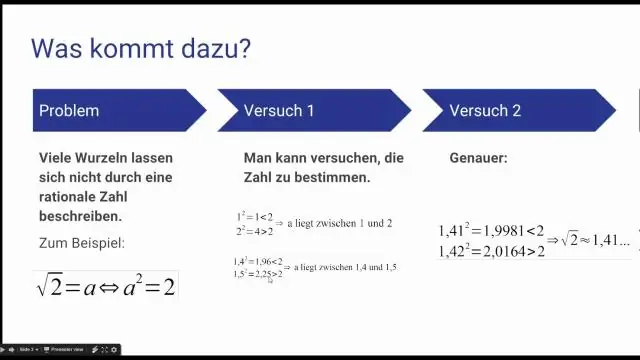
EIN Rationale Zahl ist ein Nummer das kann als das Verhältnis von zwei ganzen Zahlen ausgedrückt werden. Ebenso kann jede ganze Zahl als das Verhältnis von zwei ganzen Zahlen ausgedrückt werden, also sind alle ganzen Zahlen rational . Jedoch, Zahlen wie √2 sind irrational weil es unmöglich ist, √2 als Verhältnis von zwei ganzen Zahlen auszudrücken.
Ist 0 eine irrationale Zahl?
Irgendein Nummer was die oben genannten Bedingungen nicht erfüllt ist irrational . Was ist mit Null? Es kann als Verhältnis von zwei ganzen Zahlen sowie als Verhältnis von sich selbst und an. dargestellt werden irrationale Zahl so dass Null auf keinen Fall Dividende ist. Leute sagen, dass 0 ist rational, weil es eine ganze Zahl ist.
Empfohlen:
Sind ganze Zahlen immer manchmal oder nie rationale Zahlen?

1.5 ist eine rationale Zahl, die wie folgt geschrieben werden kann: 3/2 wobei 3 und 2 beide ganze Zahlen sind. Hier ist die rationale Zahl 8 eine ganze Zahl, aber die rationale Zahl 1,5 ist keine ganze Zahl, da 1,5 keine ganze Zahl ist. Wir können also sagen, dass eine rationale Zahl manchmal nicht immer eine ganze Zahl ist. Daher ist die richtige Antwort manchmal
Warum sind aussagekräftige Zahlen bei der Berichterstattung von Messwerten wichtig?

Signifikante Zahlen sind wichtig, um die Genauigkeit Ihrer Antwort zu zeigen. Dies ist in Wissenschaft und Technik wichtig, denn kein Messgerät kann eine Messung mit 100%iger Genauigkeit durchführen. Die Verwendung von signifikanten Zahlen ermöglicht es dem Wissenschaftler zu wissen, wie genau die Antwort ist oder wie viel Unsicherheit vorhanden ist
Welche Arten von Zahlen bilden die Menge der Zahlen, die als reelle Zahlen bezeichnet werden?

Reelle Zahlenmengen (positive ganze Zahlen) oder die ganzen Zahlen {0, 1, 2, 3,} (die nicht negativen ganzen Zahlen). Mathematiker verwenden in beiden Fällen den Begriff „natürlich“
Was sind natürliche Zahlen, ganze Zahlen, ganze Zahlen und rationale Zahlen?

Reelle Zahlen werden hauptsächlich in rationale und irrationale Zahlen eingeteilt. Rationale Zahlen umfassen alle ganzen Zahlen und Brüche. Alle negativen ganzen und ganzen Zahlen bilden die Menge der ganzen Zahlen. Ganze Zahlen bestehen aus allen natürlichen Zahlen und Null
Sind einige irrationale Zahlen ganze Zahlen?
Antwort und Erklärung: Irrationale Zahlen sind keine ganzen Zahlen. Eine irrationale Zahl ist eine Zahl, die nicht rational ist. Mit anderen Worten, eine irrationale Zahl kann nicht geschrieben werden
