Video: Was ist ein Beispiel für eine rationale Zahl, die keine ganze Zahl ist?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
EIN rational ” Nummer ist das Verhältnis zwischen zwei ganzen Zahlen. Zum Beispiel , die Folgenden sind Rationale Zahlen , und keine davon ist eine ganze Zahl: 1 / 2. 2 / 3.
Die Frage ist auch, was ist eine rationale Zahl, die keine ganze Zahl ist?
Alle negativen ganzen Zahlen sind Rationale Zahlen aber das sind keine ganzen Zahlen . Zum Beispiel -3 ist a Rationale Zahl (kann als -3/1 ausgedrückt werden, aber es ist keine ganze Zahl . Die Brüche wie 1/2, -3/4, 22/7 usw.
Zweitens, ist minus 3 eine rationale Zahl? − 3 ist negativ es ist also kein natürliches oder Ganzes Nummer . Rationale Zahlen sind Zahlen die als Bruch oder Verhältnis von zwei ganzen Zahlen ausgedrückt werden kann. Rationale Zahlen werden mit Q bezeichnet. Da − 3 kann geschrieben werden als − 3 1, könnte argumentiert werden, dass − 3 ist auch echt Nummer.
Zweitens, was ist eine rationale Zahl, die eine ganze Zahl ist?
Jeden ganze Zahl ist ein Rationale Zahl : zum Beispiel 3=31. So ist es rational . Jeden ganze Zahl n kann als Bruch von ganzen Zahlen geschrieben werden: n=n1. Wir müssen es nicht so schreiben; wir müssen nur wissen, dass es möglich ist, alles auszudrücken ganze Zahl als Bruch von ganzen Zahlen, und daher ist es rational.
Kann eine rationale Zahl eine ganze Zahl sein, aber keine ganze Zahl?
Satz von ganze Zahlen = {0, 1, 2, 3, 4, …} Ganze Zahlen sind nur ganze Zahlen die nicht negativ sind. Mit Mengennotation können wir kann sagen, dass die Menge von ganze Zahlen ist, während die Menge von ganze Zahlen ist im Grunde. Um auf die Frage zurückzukommen; Nein , Es gibt keine rationale Zahl, die keine ganze Zahl ist, aber ist ein ganze Zahl.
Empfohlen:
Was ist natürliche Zahl und ganze Zahl mit Beispiel?
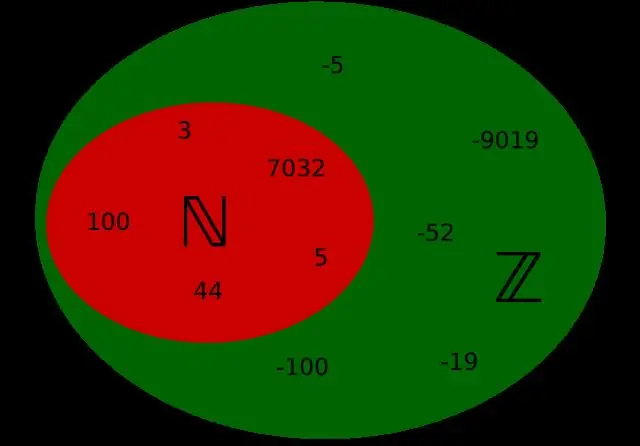
Natürliche Zahlen sind alle Zahlen 1, 2, 3, 4 … Sie zählen normalerweise und werden bis ins Unendliche fortgesetzt. Ganze Zahlen sind alle natürlichen Zahlen einschließlich 0 z.B. 0, 1, 2, 3, 4… Integers beinhalten alle ganzen Zahlen und ihr negatives Gegenstück, z.B.
Was sind natürliche Zahlen, ganze Zahlen, ganze Zahlen und rationale Zahlen?
Reelle Zahlen werden hauptsächlich in rationale und irrationale Zahlen eingeteilt. Rationale Zahlen umfassen alle ganzen Zahlen und Brüche. Alle negativen ganzen und ganzen Zahlen bilden die Menge der ganzen Zahlen. Ganze Zahlen bestehen aus allen natürlichen Zahlen und Null
Ist jede natürliche Zahl eine ganze Zahl?
Ja, das ist wahr. Denn natürliche Zahlen beginnen bei 1 und enden im Unendlichen, wobei ganze Zahlen bei 0 beginnen und im Unendlichen enden. 0 ist die einzige Zahl, die in ganzen Zahlen, aber nicht in natürlichen Zahlen enthalten ist. Daher ist jede natürliche Zahl eine ganze Zahl
Was ist eine ganze Zahl und ein Bruch?
Ja, ein Bruch kann eine ganze Zahl sein, zum Beispiel Jeder Bruch der Form a/1 = a, wobei 'a' der Zähler und 1 der Nenner ist und 'a' ein Mitglied der Menge der ganzen Zahlen ist das ist gleich {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,}
Was für eine Dezimalzahl ist eine irrationale Zahl, um ein Beispiel zu nennen?
Diese Zahlen beinhalten die nicht terminierenden, sich nicht wiederholenden Dezimalstellen (pi, 0.45445544455544445555, 2 usw.). Jede Quadratwurzel, die keine perfekte Wurzel ist, ist eine irrationale Zahl. Zum Beispiel sind 1 und 4 rational, weil 1 = 1 und 4 = 2, aber 2 und 3 sind irrational – es gibt keine perfekten Quadrate zwischen 1 und 4