Video: Was bedeutet eine negative lineare Beziehung?
2024 Autor: Miles Stephen | [email protected]. Zuletzt bearbeitet: 2023-12-15 23:32
EIN negative Korrelation bedeutet dass es eine Umkehrung gibt Beziehung zwischen zwei Variablen - wenn eine Variable abnimmt, nimmt die andere zu. Umgekehrt ist a negative Korrelation auch, bei dem eine Variable zunimmt und die andere abnimmt.
Die Leute fragen auch, was ist eine negative lineare Beziehung?
Wenn beide Variablen gleichzeitig und mit konstanter Rate steigen oder fallen, ist ein positives lineare Beziehung existiert. Wenn eine Variable zunimmt, während die andere Variable abnimmt, a negativer linearer Zusammenhang existiert.
Man kann sich auch fragen, was ist ein Beispiel für eine positive und negative Korrelation? In einem positive Korrelation , bewegen sich beide Variablen in die gleiche Richtung. Zum Beispiel , da ist ein positive Korrelation zwischen Rauchen und Alkoholkonsum. Mit dem Alkoholkonsum steigt auch das Rauchen. Wenn zwei Variablen a. haben negative Korrelation , sie haben eine umgekehrte Beziehung.
Anschließend stellt sich die Frage, wie eine negative lineare Beziehung aussieht.
Die Streuung um die Linie ist ziemlich klein, daher gibt es ein starkes lineare Beziehung . Die Steigung der Geraden ist Negativ (kleine Werte von X entsprechen großen Werten von Y; große Werte von X entsprechen kleinen Werten von Y), also gibt es a Negativ zusammen- Beziehung (das ist ein negative Korrelation ) zwischen X und Y.
Was bedeutet es, wenn der Korrelationskoeffizient negativ ist?
EIN negative Korrelation ist eine Beziehung zwischen zwei Variablen, die sich in entgegengesetzte Richtungen bewegen. Mit anderen Worten, wenn Variable A zunimmt, nimmt Variable B ab. EIN Koeffizient von -0,2 meint dass für jede Einheitsänderung in Variable B Variable A eine Abnahme erfährt, aber nur geringfügig um 0,2.
Empfohlen:
Was ist eine negative lineare Korrelation?
Eine negative Korrelation bedeutet, dass zwischen zwei Variablen eine inverse Beziehung besteht – wenn eine Variable abnimmt, steigt die andere
Was bedeutet eine schwache lineare Beziehung?
Wenn r nahe Null ist, bedeutet dies, dass die Daten eine sehr schwache lineare Beziehung oder keine lineare Beziehung haben. Wenn r nahe Null ist, ist es möglich, dass die Daten eine starke krummlinige Beziehung haben (wie wir in diesem Beispiel gesehen haben)
Was ist eine proportionale lineare Beziehung?
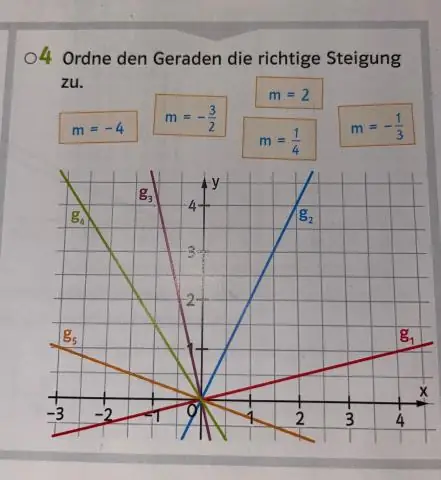
Proportionale und lineare Funktionen sind nahezu identisch. Der einzige Unterschied besteht in der Addition der Konstanten „b“zur linearen Funktion. Tatsächlich ist eine proportionale Beziehung nur eine lineare Beziehung, bei der b = 0 ist, oder anders ausgedrückt, bei der die Linie durch den Ursprung (0,0) geht
Was bedeutet es, wenn eine für beide Seiten vorteilhafte Beziehung voneinander abhängig wird?
Eine Beziehung zwischen zwei Menschen, in der jede Person von der anderen abhängig ist und von ihr positive oder negative Verstärkung erhält. jede wechselseitige oder für beide Seiten vorteilhafte Beziehung zwischen zwei Personen, Gruppen usw
Was bedeutet eine exponentielle Beziehung?
Exponentielle Beziehungen sind Beziehungen, bei denen eine der Variablen ein Exponent ist. Anstatt also '2 multipliziert mit x' zu sein, könnte eine exponentielle Beziehung '2 hoch x' haben: Normalerweise zeichnen die Leute als erstes einen Graphen, um zu verstehen, wie exponentielle Beziehungen sind